Velocidad de la onda en una cuerda bajo tensión
Para ver cómo la velocidad de una onda en una cuerda depende de la tensión y de la densidad lineal, considere un pulso enviado por una cuerda tensada (Figura \(\PageIndex{1}\)). Cuando la cuerda tensa está en reposo en la posición de equilibrio, la tensión en la cuerda \(F_T\) es constante. Consideremos un pequeño elemento de la cuerda con una masa igual a \(\Delta m = \mu \Delta x\). El elemento de masa está en reposo y en equilibrio y la fuerza de tensión de cualquier lado del elemento de masa es igual y opuesta.
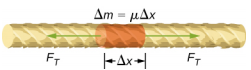
Si se puntea una cuerda bajo tensión, una onda transversal se mueve en la dirección x positiva, como se muestra en la Figura \(\PageIndex{2}\}. El elemento de masa es pequeño pero está ampliado en la figura para hacerlo visible. El pequeño elemento de masa oscila perpendicularmente al movimiento de la onda como resultado de la fuerza de restauración proporcionada por la cuerda y no se mueve en la dirección x. La tensión FT en la cuerda, que actúa en la dirección x positiva y negativa, es aproximadamente constante y es independiente de la posición y el tiempo.
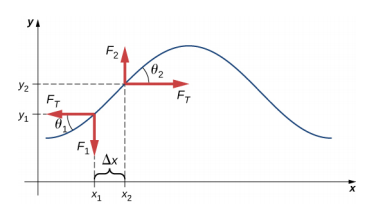
Supongamos que la inclinación de la cuerda desplazada con respecto al eje horizontal es pequeña. La fuerza neta sobre el elemento de la cuerda, que actúa paralela a la misma, es la suma de la tensión en la cuerda y la fuerza restauradora. Las componentes x de la fuerza de tensión se cancelan, por lo que la fuerza neta es igual a la suma de las componentes y de la fuerza. La magnitud de la componente x de la fuerza es igual a la fuerza horizontal de tensión de la cuerda \(F_T\) como se muestra en la Figura \(\PageIndex{2}\). Para obtener los componentes y de la fuerza, observe que tan \\ta_{1} = – \frac{F_{1}}{F_{T}}) y \tan \ta_{2} = \frac{F_{2}}{F_{T}}). El \(\tan \theta\}) es igual a la pendiente de una función en un punto, que es igual a la derivada parcial de y con respecto a x en ese punto. Por tanto, \(\frac{F_{1}}{F_{T}}) es igual a la pendiente negativa de la cuerda en x1 y \(\frac{F_{T}}) es igual a la pendiente de la cuerda en x2:
La fuerza neta es sobre el elemento de masa pequeña puede escribirse como
\ \ldotp]
Utilizando la segunda ley de Newton, la fuerza neta es igual a la masa por la aceleración. La densidad lineal de la cuerda µ es la masa por longitud de la cuerda, y la masa de la porción de la cuerda es \(\mu \Delta\)x,
Se divide por FT(\mu \Delta)x y se toma el límite a medida que \ {parcial^{2} y} {parcial t^{2}} se aproxima a cero,
{Delta x} & = \frac {\mu}{F_{T}} \y}{parcial t^2}{parcial t^2} \\ y} {parcial x^2} & = \frac{\mu}{F_{T}} \y}{parcial t^2}{parcial t^2} \ldotp \end{split}]
Recordemos que la ecuación de onda lineal es
Por lo tanto,
Resolviendo para \\ v vemos que la velocidad de la onda en una cuerda depende de la tensión y de la densidad lineal
Velocidad de una onda en una cuerda bajo tensión
La velocidad de un pulso u onda en una cuerda bajo tensión se puede encontrar con la ecuación
donde \(F_T\) es la tensión en la cuerda y \(µ\) es la masa por longitud de la cuerda.
En una guitarra de seis cuerdas, la cuerda E alta tiene una densidad lineal de \(\mu_{Alta; E}\) = 3,09 x 10-4 kg/m y la cuerda E baja tiene una densidad lineal de \(\mu_{Baja; E}\) = 5,78 x 10-3 kg/m. (a) Si se puntea la cuerda de alto E, produciendo una onda en la cuerda, ¿cuál es la velocidad de la onda si la tensión de la cuerda es de 56,40 N? (b) La densidad lineal de la cuerda de mi grave es aproximadamente 20 veces mayor que la de la cuerda de mi agudo. Para que las ondas viajen a través de la cuerda E baja con la misma velocidad de onda que la cuerda E alta, ¿tendría que ser la tensión mayor o menor que la de la cuerda E alta? ¿Cuál sería la tensión aproximada? (c) Calcula la tensión de la cuerda de baja E necesaria para la misma velocidad de onda.
Estrategia
- La velocidad de la onda se puede hallar a partir de la densidad lineal y de la tensión \N(v = \sqrt{\frac{F_{T}{\mu}}).
- A partir de la ecuación v = \(\sqrt{\frac{F_{T}{mu}}), si la densidad lineal se incrementa en un factor de casi 20, la tensión tendría que incrementarse en un factor de 20.
- Conociendo la velocidad y la densidad lineal, se puede resolver la ecuación de la velocidad para la fuerza de tensión FT = \(\mu\)v2.
- Utilizar la ecuación de la velocidad para encontrar la velocidad: $$v = \sqrt{\frac{F_{T}}{mu}} = \sqrt{\frac{56.40\; N}{3,09 \times 10^{-4}\; kg/m}} = 427,23\; m/s \ldotp$$
- Habría que aumentar la tensión en un factor de aproximadamente 20. La tensión sería ligeramente inferior a 1128 N.
- Utiliza la ecuación de la velocidad para encontrar la tensión real: $$F_{T} = \mu v^{2} = (5,78 \times 10^{-3}}}(427,23\; m/s)^{2} = 1055,00\; N \ldotp$$
- Esta solución está dentro del 7% de la aproximación.
Solución
Significado
Las notas estándar de las seis cuerdas (Mi agudo, Si, Sol, Re, La, Mi grave) están afinadas para vibrar a las frecuencias fundamentales (329,63 Hz, 246,94 Hz, 196,00 Hz, 146,83 Hz, 110,00 Hz y 82,41 Hz) al ser punteadas. Las frecuencias dependen de la velocidad de las ondas en la cuerda y de la longitud de onda de las mismas. Las seis cuerdas tienen diferentes densidades lineales y se «afinan» cambiando las tensiones en las cuerdas. Veremos en Interferencia de ondas que la longitud de onda depende de la longitud de las cuerdas y de las condiciones de contorno. Para tocar notas distintas a las fundamentales, se cambian las longitudes de las cuerdas presionándolas.
La velocidad de la onda en una cuerda depende de la tensión y de la densidad lineal de masa. Si se duplica la tensión, ¿qué ocurre con la velocidad de las ondas sobre la cuerda?