Objectifs d’apprentissage
À la fin de cette section, vous serez en mesure de :
- Exprimer la densité d’énergie moyennée dans le temps des ondes électromagnétiques en termes d’amplitudes de leurs champs électrique et magnétique
- Calculer le vecteur de Poynting et l’intensité énergétique des ondes électromagnétiques
- Expliquer comment l’énergie d’une onde électromagnétique dépend de son amplitude, alors que l’énergie d’un photon est proportionnelle à sa fréquence
Toute personne ayant utilisé un four à micro-ondes sait qu’il y a de l’énergie dans les ondes électromagnétiques. Parfois, cette énergie est évidente, comme dans la chaleur du Soleil d’été. D’autres fois, elle est subtile, comme l’énergie non ressentie des rayons gamma, qui peuvent détruire les cellules vivantes.
Les ondes électromagnétiques apportent de l’énergie dans un système en vertu de leurs champs électriques et magnétiques. Ces champs peuvent exercer des forces et déplacer des charges dans le système et, ainsi, effectuer un travail sur elles. Cependant, il y a de l’énergie dans une onde électromagnétique elle-même, qu’elle soit absorbée ou non. Une fois créés, les champs transportent l’énergie à partir d’une source. Si une partie de l’énergie est absorbée par la suite, les forces des champs sont diminuées et tout ce qui reste voyage sur.
Il est clair que plus la force des champs électriques et magnétiques est grande, plus ils peuvent faire du travail et plus l’énergie que l’onde électromagnétique transporte est grande. Dans les ondes électromagnétiques, l’amplitude est l’intensité maximale des champs électriques et magnétiques (figure \(\PageIndex{1}\)). L’énergie de l’onde est déterminée par l’amplitude de l’onde.
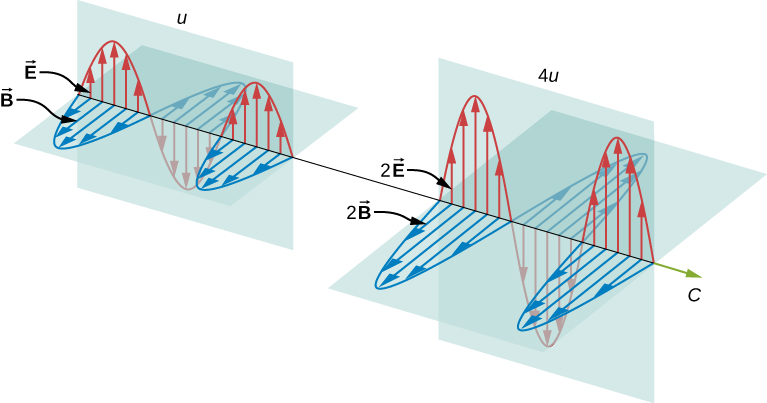
Pour une onde plane se propageant dans la direction de l’axe x positif, la phase de l’onde étant choisie de telle sorte que le maximum de l’onde soit à l’origine à \(t = 0\), les champs électriques et magnétiques obéissent aux équations
\
L’énergie d’une partie quelconque de l’onde électromagnétique est la somme des énergies des champs électriques et magnétiques. Cette énergie par unité de volume, ou densité d’énergie u, est la somme de la densité d’énergie du champ électrique et de la densité d’énergie du champ magnétique. Les expressions des deux densités d’énergie des champs ont été abordées précédemment (\(u_E\) pour la capacité et \(u_B\) pour l’inductance). En combinant ces contributions, nous obtenons
L’expression \(E = cB = \frac{1}{\sqrt{\epsilon_0\mu_0}}B\) montre alors que la densité d’énergie magnétique \(u_B\) et la densité d’énergie électrique \(u_E\) sont égales, malgré le fait que les champs électriques changeants ne produisent généralement que de petits champs magnétiques. L’égalité des densités d’énergie électrique et magnétique conduit à
La densité d’énergie se déplace avec les champs électriques et magnétiques de manière similaire aux ondes elles-mêmes.
Nous pouvons trouver le taux de transport de l’énergie en considérant un petit intervalle de temps \(\Delta t\). Comme le montre la figure \(\PageIndex{2}\), l’énergie contenue dans un cylindre de longueur \(c\Delta t\) et d’aire de section A passe par le plan de section dans l’intervalle \(\Delta t\).
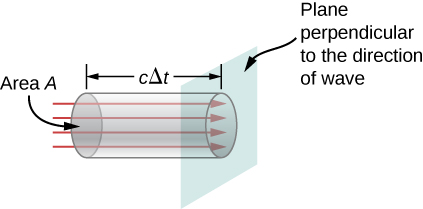
L’énergie traversant l’aire \(A\) en un temps \(\Delta t\) est
L’énergie par unité de surface par unité de temps passant par un plan perpendiculaire à l’onde, appelée flux énergétique et notée \(S\), peut être calculée en divisant l’énergie par la surface \(A\) et l’intervalle de temps \(\Delta t\).
Plus généralement, le flux d’énergie à travers une surface quelconque dépend aussi de l’orientation de cette surface. Pour tenir compte de la direction, nous introduisons un vecteur \(\vec{S}\), appelé vecteur de Poynting, avec la définition suivante :
Le produit en croix de \(\vec{E}\) et \(\vec{B}\) pointe dans la direction perpendiculaire aux deux vecteurs. Pour confirmer que la direction de \(\vec{S}\) est celle de la propagation de l’onde, et non sa négative, revenez à la figure 16.3.2. Notez que les lois de Lenz et de Faraday impliquent que lorsque le champ magnétique représenté est croissant dans le temps, le champ électrique est plus grand en \(x\) qu’en \(x + \Delta x\). Le champ électrique diminue avec l’augmentation de \(x\) au moment et à l’endroit donnés. La proportionnalité entre les champs électrique et magnétique exige que le champ électrique augmente dans le temps en même temps que le champ magnétique. Ceci n’est possible que si l’onde se propage vers la droite sur le schéma, auquel cas, les orientations relatives montrent que \(\vec{S} = \frac{1}{\mu_0} \vec{E} \times \vec{B}\) est spécifiquement dans la direction de propagation de l’onde électromagnétique.
Le flux d’énergie en tout lieu varie également dans le temps, comme on peut le voir en substituant \(u\) de l’équation 16.3.19 dans l’équation \ref{16.27}.
Parce que la fréquence de la lumière visible est très élevée, de l’ordre de \(10^{14} \, Hz\), le flux d’énergie pour la lumière visible à travers n’importe quelle zone est une quantité variant extrêmement rapidement. La plupart des appareils de mesure, y compris nos yeux, ne détectent qu’une moyenne sur de nombreux cycles. La moyenne temporelle du flux énergétique est l’intensité \(I\) de l’onde électromagnétique et est la puissance par unité de surface. On peut l’exprimer en faisant la moyenne de la fonction cosinus de l’équation \ref{16.29} sur un cycle complet, ce qui revient à faire la moyenne temporelle sur plusieurs cycles (ici, \(T\) est une période) :
Nous pouvons soit évaluer l’intégrale, soit noter que puisque le sinus et le cosinus diffèrent simplement en phase, la moyenne sur un cycle complet pour \(cos^2 \, (\xi)\) est la même que pour \(sin^2 \, (\xi)\), pour obtenir
\ = \frac{1}{2}. \langle 1 \rangle = \frac{1}{2}.\]
où les crochets \(\langle . . . \rangle \) représentent l’opération de moyennage temporel. On trouve alors que l’intensité de la lumière se déplaçant à la vitesse \(c\) dans le vide est
en termes d’intensité maximale du champ électrique \(E_0\), qui est aussi l’amplitude du champ électrique. Une manipulation algébrique produit la relation
\
où \(B_0\) est l’amplitude du champ magnétique, qui est la même que l’intensité maximale du champ magnétique. Une autre expression pour \(I_{avg}\) en termes d’intensité de champ électrique et magnétique est utile. En substituant le fait que \(cB_0 = E_0\), l’expression précédente devient
Nous pouvons utiliser celle des trois équations précédentes qui nous convient le mieux, car les trois équations ne sont en fait que des versions différentes du même résultat : L’énergie d’une onde est liée à l’amplitude au carré. De plus, comme ces équations sont basées sur l’hypothèse que les ondes électromagnétiques sont sinusoïdales, l’intensité de crête est le double de l’intensité moyenne ; c’est-à-dire \(I_0 = 2I\).
Exemple \(\PageIndex{1}\) : Un faisceau laser
Le faisceau d’un petit laser de laboratoire a généralement une intensité d’environ \(1,0 \times 10^{-3} W/m^2\). En supposant que le faisceau est composé d’ondes planes, calculez les amplitudes des champs électrique et magnétique dans le faisceau.
Stratégie
Utiliser l’équation exprimant l’intensité en termes de champ électrique pour calculer le champ électrique à partir de l’intensité.
Solution
D’après l’équation \ref{16.31}, l’intensité du faisceau laser est
L’amplitude du champ électrique est donc
\ &= \sqrt{\frac{2}{(3.00 \times 10^8 m/s)(8.85 \times 10^{-12} F/m)}\left(1.0 \times 10^{-3} W/m^2 \right)} \\N &= 0.87 \, V/m. \end{align*}\]
L’amplitude du champ magnétique peut être obtenue à partir de :
Champs d’une ampoule électrique
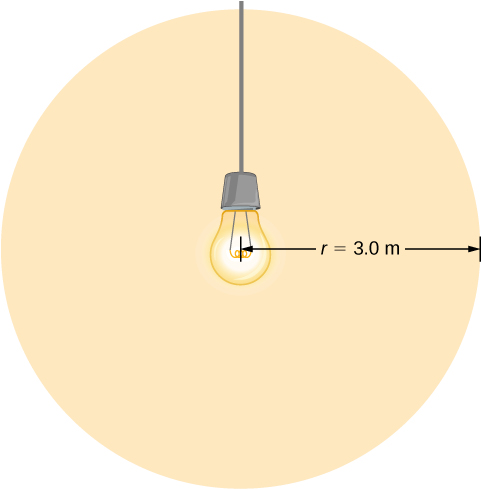
Une ampoule électrique émet 5,00 W de puissance sous forme de lumière visible. Quels sont les champs électriques et magnétiques moyens de cette lumière à une distance de 3,0 m ?
Stratégie
Supposons que la puissance de sortie P de l’ampoule soit répartie uniformément sur une sphère de rayon 3,0 m pour calculer l’intensité, et à partir de celle-ci, le champ électrique.
Solution
La puissance rayonnée sous forme de lumière visible est alors
\(I = \frac{P}{4\pi r^2} = \frac{c\epsilon_0 E_0^2}{2},
(E_0 = \sqrt{2\frac{P}{4\pi r^2} c\epsilon_0} = \sqrt{2\frac{5.00 \, W}{4\pi (3.0 \, m)^2 (3.00 \times 10^8 \, m/s)(8.85 \times 10^{-12} C^2/N \cdot m^2)}} = 5.77 \, N/C,\)
\(B_0 = E_0/c = 1,92 \times 10^{-8} \, T\).
Signification
L’intensité I décroît avec le carré de la distance si le rayonnement est dispersé uniformément dans toutes les directions.
Distance radio
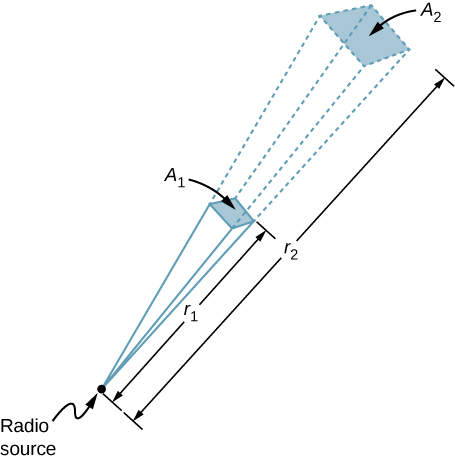
Un émetteur radio de 60 kW sur Terre envoie son signal à un satellite situé à 100 km de là (figure \(\PageIndex{3}\)). À quelle distance, dans la même direction, le signal aurait-il le même champ maximal si la puissance de sortie de l’émetteur était portée à 90 kW ?
Stratégie
La zone sur laquelle se disperse la puissance dans une direction particulière augmente avec le carré de la distance, comme l’illustre la figure \(\PageIndex{3}\). Modifiez la puissance de sortie P par un facteur de (90 kW/60 kW) et modifiez la surface par le même facteur pour que \(I = \frac{P}{A} = \frac{c\epsilon_0 E_0^2}{2}\) reste identique. Utilisez ensuite la proportion de l’aire A du diagramme par rapport à la distance au carré pour trouver la distance qui produit le changement d’aire calculé.
Solution
En utilisant la proportionnalité des aires aux carrés des distances, et en résolvant, on obtient à partir du diagramme
\ r_2 &= \sqrt{\frac{90}{60}}(100 \, km) \\\ &= 122 \, km. \end{align*}\]
Signification
La portée d’un signal radio est la distance maximale entre l’émetteur et le récepteur qui permet un fonctionnement normal. En l’absence de complications telles que les réflexions sur les obstacles, l’intensité suit une loi carrée inverse, et doubler la portée nécessiterait de multiplier la puissance par quatre.
Contributeurs et attributions
-
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University) et Bill Moebs avec de nombreux auteurs collaborateurs. Ce travail est autorisé par OpenStax University Physics sous une licence Creative Commons Attribution License (by 4.0).
.