Tanulmányi célok
A szakasz végére képesek leszünk:
- Kifejtse az elektromágneses hullámok időátlagolt energiasűrűségét az elektromos és mágneses tér amplitúdójának függvényében
- Kiszámítsa a Poynting-vektort és az elektromágneses hullámok energiaintenzitását
- Magyarázza, hogy az elektromágneses hullám energiája az amplitúdójától függ, míg a foton energiája a frekvenciájával arányos
Aki használt már mikrohullámú sütőt, tudja, hogy az elektromágneses hullámokban energia van. Néha ez az energia nyilvánvaló, például a nyári Nap melegében. Máskor viszont finom, mint például a gammasugarak nem érezhető energiája, amely képes elpusztítani az élő sejteket.
Az elektromágneses hullámok elektromos és mágneses mezejük révén energiát visznek egy rendszerbe. Ezek a mezők erőket fejthetnek ki és mozgathatják a rendszerben lévő töltéseket, és így munkát végezhetnek rajtuk. Az elektromágneses hullám azonban magában az elektromágneses hullámban is van energia, akár elnyelődik, akár nem. A mezők, ha egyszer létrejönnek, energiát visznek el a forrástól. Ha később elnyelődik némi energia, a mezők erőssége csökken, és ami megmarad, az továbbvándorol.
Látható, hogy minél nagyobb az elektromos és mágneses mezők erőssége, annál több munkát tudnak végezni, és annál nagyobb energiát hordoz az elektromágneses hullám. Az elektromágneses hullámoknál az amplitúdó az elektromos és mágneses mezők maximális térerőssége (\(\PageIndex{1}\) ábra). A hullám energiáját a hullám amplitúdója határozza meg.
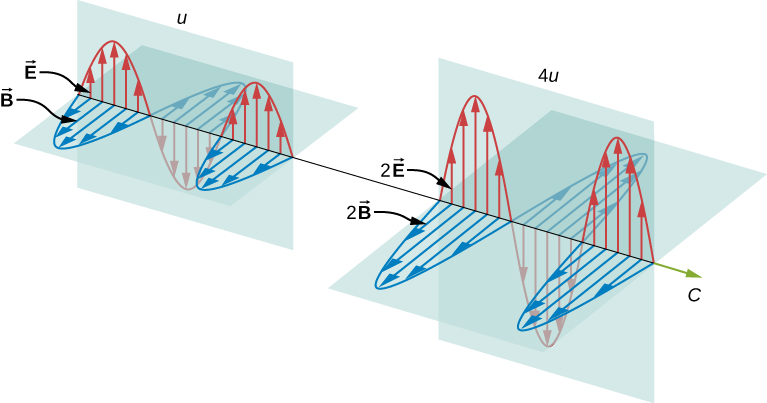
A pozitív x-tengely irányában haladó síkhullám esetében, amelynek fázisát úgy választjuk meg, hogy a hullám maximuma az \(t = 0\) origóban legyen, az elektromos és mágneses mezők az egyenleteknek engedelmeskednek
\
\
Az elektromágneses hullám bármely részének energiája az elektromos és mágneses mezők energiáinak összege. Ez az egységnyi térfogatra jutó energia vagy u energiasűrűség az elektromos mezőből származó energiasűrűség és a mágneses mezőből származó energiasűrűség összege. A két mező energiasűrűségére vonatkozó kifejezéseket korábban már tárgyaltuk (\(u_E\) a kapacitásra és \(u_B\) az induktivitásra). Ezeket a hozzájárulásokat kombinálva megkapjuk
\
Az \(E = cB = \frac{1}{\sqrt{\epsilon_0\mu_0}}B\) kifejezés azt mutatja, hogy a mágneses energiasűrűség \(u_B\) és az elektromos energiasűrűség \(u_E\) egyenlő, annak ellenére, hogy a változó elektromos mezők általában csak kis mágneses tereket eredményeznek. Az elektromos és mágneses energiasűrűség egyenlőségéből következik, hogy
\
Az energiasűrűség az elektromos és mágneses mezőkkel együtt mozog, hasonló módon, mint maguk a hullámok.
Az energia terjedési sebességét egy kis időintervallum \(\Delta t\) figyelembevételével találhatjuk meg. Ahogy az \(\PageIndex{2}\) ábrán látható, egy \(c\Delta t\) hosszúságú és A keresztmetszetű hengerben lévő energia az \(\Delta t\) intervallumban halad át a keresztmetszeti síkon.
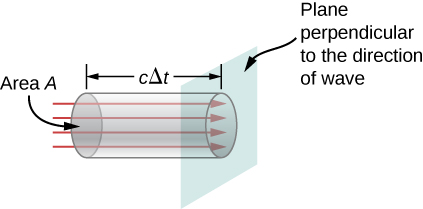
Az \(A\) területen \(\Delta t\) idő alatt áthaladó energia
\
A hullámra merőleges síkon egységnyi idő alatt egységnyi területen áthaladó energia, amelyet energiaáramlásnak nevezünk és \(S\)-vel jelölünk, kiszámítható, ha az energiát elosztjuk az \(A\) területtel és az \(\Delta t\) időintervallummal.
Általánosabban, az energiaáramlás bármely felületen keresztül a felület tájolásától is függ. Az irány figyelembevételére bevezetünk egy \(\vec{S}\) vektort, az úgynevezett Poynting-vektort, a következő definícióval:
\
Az \(\vec{E}\) és \(\vec{B}\) keresztprodukciója a két vektorra merőleges irányba mutat. Annak megerősítésére, hogy az \(\vec{S}\) iránya a hullám terjedésének iránya, és nem a negatívja, térjünk vissza a 16.3.2. ábrára. Vegyük észre, hogy Lenz és Faraday törvényeiből következik, hogy amikor a mágneses mező időben növekszik, az elektromos mező nagyobb az \(x\) pontban, mint az \(x + \Delta x\) pontban. Az elektromos mező az \(x\) növekedésével csökken az adott időben és helyen. Az elektromos és mágneses mezők közötti arányosság megköveteli, hogy az elektromos mező az időben a mágneses mezővel együtt növekedjen. Ez csak akkor lehetséges, ha a hullám az ábrán jobbra terjed, ebben az esetben a relatív orientációk azt mutatják, hogy \(\vec{S} = \frac{1}{\mu_0} \vec{E} \times \vec{B}\) kifejezetten az elektromágneses hullám terjedési irányában van.
Az energiaáramlás bármely helyen időben is változik, amint az látható, ha a 16.3.19. egyenletből \(u\) értékét behelyettesítjük a \ref{16.27} egyenletbe.
Mivel a látható fény frekvenciája nagyon magas, \(10^{14} \, Hz\) nagyságrendű, a látható fény energiaáramlása bármely területen keresztül rendkívül gyorsan változó mennyiség. A legtöbb mérőeszköz, beleértve a szemünket is, csak sok ciklus átlagát érzékeli. Az energiaáram időbeli átlaga az elektromágneses hullám \(I\) intenzitása és az egységnyi területre jutó teljesítmény. Kifejezhető a \ref{16.29} egy teljes cikluson keresztül, ami megegyezik a sok cikluson keresztüli időátlagolással (itt \(T\) egy periódus):
\
Vagy kiértékeljük az integrált, vagy megjegyezzük, hogy mivel a szinusz és a koszinusz csak a fázisban különbözik, az \(cos^2 \, (\xi)\) egy teljes ciklusra vonatkozó átlaga megegyezik az \(sin^2 \, (\xi)\) esetében, így megkapjuk
\ = \frac{1}{2} \langle 1 \rangle = \frac{1}{2}.\]
ahol a szögletes zárójelek \(\langle . . . . \rangle \) az időátlagolási műveletet jelölik. A vákuumban \(c\) sebességgel mozgó fény intenzitását ezután úgy találjuk, hogy
\
a maximális elektromos térerősség \(E_0\), amely egyben az elektromos tér amplitúdója is. Algebrai manipulációval megkapjuk az összefüggést
\
ahol \(B_0\) a mágneses tér amplitúdója, ami megegyezik a maximális mágneses térerősséggel. Hasznos még egy kifejezés az \(I_{avg}\) számára mind az elektromos, mind a mágneses térerősség szempontjából. Behelyettesítve azt a tényt, hogy \(cB_0 = E_0\), az előző kifejezés a következővé válik
\
Az előző három egyenlet közül bármelyiket használhatjuk, amelyik a legkényelmesebb, mert a három egyenlet valójában csak ugyanannak az eredménynek a különböző változatai: A hullám energiája az amplitúdó négyzetével függ össze. Továbbá, mivel ezek az egyenletek azon a feltételezésen alapulnak, hogy az elektromágneses hullámok szinuszosak, a csúcsintenzitás az átlagos intenzitás kétszerese, azaz \(I_0 = 2I\).
Példa \(\PageIndex{1}\): A lézersugár
A kis laboratóriumi lézernyaláb intenzitása jellemzően körülbelül \(1,0 \szor 10^{-3} W/m^2\). Feltételezve, hogy a sugár síkhullámokból áll, számítsuk ki a sugárban lévő elektromos és mágneses tér amplitúdóit.
Stratégia
Az intenzitást az elektromos térrel kifejező egyenlet segítségével számítsuk ki az intenzitásból az elektromos teret.
megoldás
Az \ref{16.31} egyenletből a lézersugár intenzitása
\
Az elektromos mező amplitúdója tehát
\ &= \sqrt{\frac{2}{(3.00 \times 10^8 m/s)(8.85 \times 10^{-12} F/m)}\left(1.0 \times 10^{-3} W/m^2 \right)}\left(1.0 \times 10^{-3} W/m^2 \right)} \\ &= 0,87 \, V/m. \end{align*}\]
A mágneses mező amplitúdóját a következőkből kaphatjuk:
Lámpás mezők
A villanykörte 5,00 W teljesítményt bocsát ki látható fény formájában. Mekkora a fény átlagos elektromos és mágneses tere 3,0 m távolságban?
Stratégia
Tegyük fel, hogy az izzó P teljesítménye egyenletesen oszlik el egy 3,0 m sugarú gömbön, hogy kiszámítsuk az intenzitást, és ebből az elektromos mezőt.
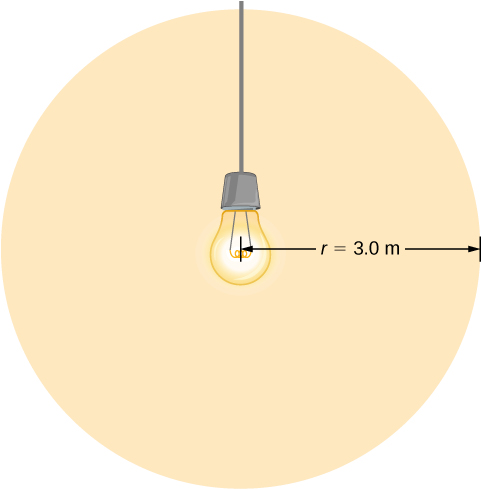
megoldás
A látható fényként kisugárzott teljesítmény ekkor
\(I = \frac{P}{4\pi r^2} = \frac{c\epsilon_0 E_0^2}{2},\)
\(E_0 = \sqrt{2\frac{P}{4\pi r^2 c\epsilon_0}} = \sqrt{2\frac{5.00 \, W}{4\pi (3.0 \, m)^2 (3.00 \times 10^8 \, m/s)(8.85 \times 10^{-12} C^2/N \cdot m^2)}} = 5.77 \, N/C,\)
\(B_0 = E_0/c = 1,92 \times 10^{-8} \, T\).
Szignifikancia
A távolság négyzetével csökken az intenzitás I, ha a sugárzás minden irányban egyenletesen szóródik.
Rádió hatótávolság
Egy 60 kW-os rádióadó a Földön egy 100 km-re lévő műholdra küldi a jelét (\(\(\PageIndex{3}\) ábra). Ugyanabban az irányban milyen távolságban lenne ugyanolyan maximális térerősségű a jel, ha az adó kimenő teljesítményét 90 kW-ra növelnénk?
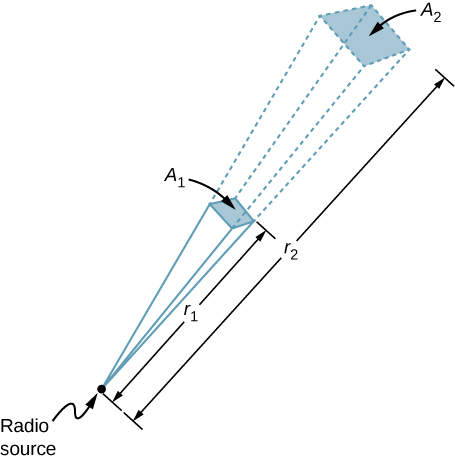
Stratégia
Az \(\PageIndex{3}\) ábra szerint a távolság négyzetével nő az a terület, amelyen a teljesítmény egy adott irányban szétszóródik. Változtassuk meg a P kimenő teljesítményt a (90 kW/60 kW) tényezővel, és változtassuk meg a területet ugyanezzel a tényezővel, hogy \(I = \frac{P}{A} = \frac{c\epsilon_0 E_0^2}{2}\) változatlan maradjon. Ezután az ábrán az A területnek a távolság négyzetéhez viszonyított arányát használjuk, hogy megtaláljuk azt a távolságot, amely a kiszámított területváltozást eredményezi.
megoldás
A területeknek a távolságok négyzetéhez való arányosságát felhasználva és megoldva az ábrából
\ r_2 &= \sqrt{\frac{90}{60}}}(100 \, km) \\\ &= 122 \, km. \end{align*}\]
Meghatározás
A rádiójel hatótávolsága az adó és a vevő közötti maximális távolság, amely lehetővé teszi a normál működést. Bonyodalmak, például az akadályokról való visszaverődések hiányában az intenzitás a fordított négyzetes törvényt követi, és a hatótávolság megduplázásához a teljesítmény négyszeresére lenne szükség.
Munkatársak és hozzászólások
-
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University) és Bill Moebs számos közreműködő szerzővel. Ezt a munkát az OpenStax University Physics licenceli a Creative Commons Attribution License (by 4.0) alatt.
/div>