Obiettivi di apprendimento
Alla fine di questa sezione, sarete in grado di:
- Esprimere la densità di energia mediata nel tempo delle onde elettromagnetiche in termini delle loro ampiezze di campo elettrico e magnetico
- Calcolare il vettore Poynting e l’intensità di energia delle onde elettromagnetiche
- Spiegare come l’energia di un’onda elettromagnetica dipende dalla sua ampiezza, mentre l’energia di un fotone è proporzionale alla sua frequenza
Chiunque abbia usato un forno a microonde sa che c’è energia nelle onde elettromagnetiche. A volte questa energia è evidente, come nel calore del sole estivo. Altre volte, è sottile, come l’energia non percepita dei raggi gamma, che possono distruggere le cellule viventi.
Le onde elettromagnetiche portano energia in un sistema in virtù dei loro campi elettrici e magnetici. Questi campi possono esercitare forze e spostare cariche nel sistema e, quindi, fare lavoro su di esse. Tuttavia, c’è energia in un’onda elettromagnetica stessa, sia che venga assorbita o meno. Una volta creati, i campi portano via l’energia da una fonte. Se una parte dell’energia viene poi assorbita, l’intensità del campo diminuisce e tutto ciò che rimane viaggia su di esso.
Chiaramente, maggiore è la forza dei campi elettrici e magnetici, più lavoro possono fare e maggiore è l’energia che l’onda elettromagnetica porta. Nelle onde elettromagnetiche, l’ampiezza è l’intensità massima dei campi elettrici e magnetici (Figura \PageIndex{1}}). L’energia dell’onda è determinata dall’ampiezza dell’onda.
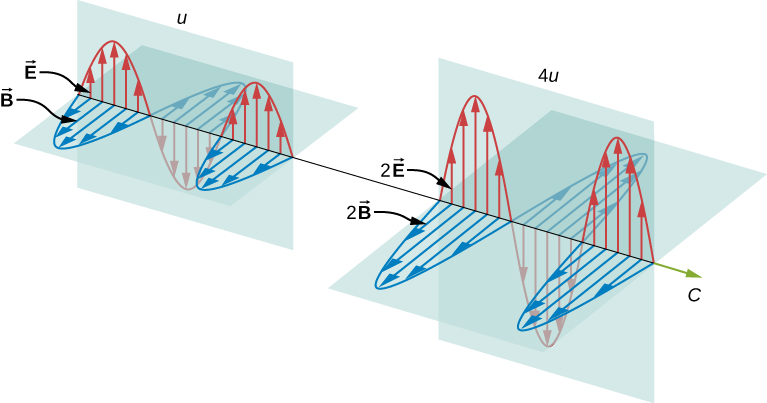
Per un’onda piana che viaggia nella direzione dell’asse x positivo con la fase dell’onda scelta in modo che il massimo dell’onda sia all’origine in \(t = 0\), i campi elettrico e magnetico obbediscono alle equazioni
L’energia in qualsiasi parte dell’onda elettromagnetica è la somma delle energie dei campi elettrico e magnetico. Questa energia per unità di volume, o densità di energia u, è la somma della densità di energia del campo elettrico e della densità di energia del campo magnetico. Le espressioni per entrambe le densità di energia del campo sono state discusse in precedenza (\(u_E\) nella capacità e \(u_B\) nell’induttanza). Combinando questi contributi, otteniamo
L’espressione \(E = cB = \frac{1}{sqrt{epsilon_0\mu_0}}B\) mostra quindi che la densità di energia magnetica \(u_B\) e la densità di energia elettrica \(u_E\) sono uguali, nonostante il fatto che i campi elettrici variabili producono generalmente solo piccoli campi magnetici. L’uguaglianza delle densità di energia elettrica e magnetica porta a
La densità di energia si muove con i campi elettrici e magnetici in modo simile alle onde stesse.
Possiamo trovare la velocità di trasporto dell’energia considerando un piccolo intervallo di tempo \(\Delta t\). Come mostrato nella figura \(\PageIndex{2}), l’energia contenuta in un cilindro di lunghezza \(c\Delta t\) e area di sezione A passa attraverso il piano trasversale nell’intervallo \(\Delta t\).
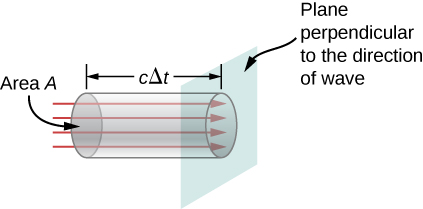
L’energia che passa attraverso l’area \(A\) nel tempo \(\Delta t\) è
L’energia per unità di area per unità di tempo che passa attraverso un piano perpendicolare all’onda, chiamato flusso di energia e indicato con \(S\), può essere calcolato dividendo l’energia per l’area \(A\) e l’intervallo di tempo \(\Delta t\).
Più in generale, il flusso di energia attraverso qualsiasi superficie dipende anche dall’orientamento della superficie. Per tenere conto della direzione, introduciamo un vettore \(\vec{S}\ chiamato vettore di Poynting, con la seguente definizione:
Il prodotto incrociato di \(\vec{E}\ e \(\vec{B}\ punta nella direzione perpendicolare a entrambi i vettori. Per confermare che la direzione di \(\vec{S}}) è quella della propagazione dell’onda, e non il suo negativo, torna alla figura 16.3.2. Si noti che le leggi di Lenz e Faraday implicano che quando il campo magnetico indicato è crescente nel tempo, il campo elettrico è maggiore in \(x\) che in \(x + \Delta x\). Il campo elettrico è decrescente con l’aumento di \(x\) in un dato tempo e luogo. La proporzionalità tra campi elettrici e magnetici richiede che il campo elettrico aumenti nel tempo insieme al campo magnetico. Questo è possibile solo se l’onda si sta propagando verso destra nel diagramma, nel qual caso, gli orientamenti relativi mostrano che \(\vec{S} = \frac{1}{mu_0} \vec{E} \volte \vec{B}) è specificamente nella direzione di propagazione dell’onda elettromagnetica.
Il flusso di energia in qualsiasi luogo varia anche nel tempo, come si può vedere sostituendo \(u) dall’equazione 16.3.19 nell’equazione \ref{16.27}.
Perché la frequenza della luce visibile è molto alta, dell’ordine di \(10^{14} \, Hz\), il flusso di energia per la luce visibile attraverso qualsiasi area è una quantità che varia molto rapidamente. La maggior parte dei dispositivi di misurazione, compresi i nostri occhi, rilevano solo una media su molti cicli. La media temporale del flusso di energia è l’intensità \(I\) dell’onda elettromagnetica ed è la potenza per unità di superficie. Può essere espressa facendo la media della funzione coseno nell’equazione 16.29} su un ciclo completo, che è lo stesso della media temporale su molti cicli (qui, \(T\) è un periodo):
Possiamo valutare l’integrale, oppure notare che poiché il seno e il coseno differiscono solo per la fase, la media su un ciclo completo per \(cos^2 \, (\xi)\) è la stessa di \(sin^2 \, (\xi)\), per ottenere
= \frac{1}{2} \langolo 1 \rangolo = \frac{1}{2}.\]
dove le parentesi angolari \(\langolo . . . \rangolo \) stanno per l’operazione di mediazione temporale. L’intensità della luce che si muove a velocità \(c\) nel vuoto si trova quindi ad essere
\
in termini di intensità massima del campo elettrico \(E_0\), che è anche l’ampiezza del campo elettrico. La manipolazione algebrica produce la relazione
dove \(B_0\) è l’ampiezza del campo magnetico, che è la stessa dell’intensità massima del campo magnetico. Un’altra espressione per \(I_{avg}\ in termini di intensità di campo elettrico e magnetico è utile. Sostituendo il fatto che \(cB_0 = E_0\), l’espressione precedente diventa
\
Possiamo usare qualsiasi delle tre equazioni precedenti sia più conveniente, perché le tre equazioni sono in realtà solo versioni diverse dello stesso risultato: L’energia in un’onda è legata all’ampiezza al quadrato. Inoltre, poiché queste equazioni si basano sull’assunzione che le onde elettromagnetiche siano sinusoidali, l’intensità di picco è il doppio dell’intensità media; cioè, \(I_0 = 2I\).
Esempio \(\PageIndex{1}): Un raggio laser
Il raggio di un piccolo laser da laboratorio ha tipicamente un’intensità di circa \(1,0 \volte 10^{-3} W/m^2\). Assumendo che il raggio sia composto da onde piane, calcola le ampiezze dei campi elettrici e magnetici nel raggio.
Strategia
Usa l’equazione che esprime l’intensità in termini di campo elettrico per calcolare il campo elettrico dall’intensità.
Soluzione
Dall’equazione \ref{16.31}, l’intensità del raggio laser è
L’ampiezza del campo elettrico è quindi
&= \sqrt{frac{2}(3.00 volte 10^8 m/s)(8,85 volte 10^{-12} F/m)} a sinistra(1,0 volte 10^{-3} W/m^2 a destra)} &= 0,87 \V/m.
L’ampiezza del campo magnetico può essere ottenuta da:
Campi delle lampadine
Una lampadina emette 5,00 W di potenza come luce visibile. Quali sono i campi elettrici e magnetici medi della luce ad una distanza di 3,0 m?
Strategia
Assumiamo che la potenza di uscita P della lampadina sia distribuita uniformemente su una sfera di raggio 3,0 m per calcolare l’intensità, e da essa, il campo elettrico.
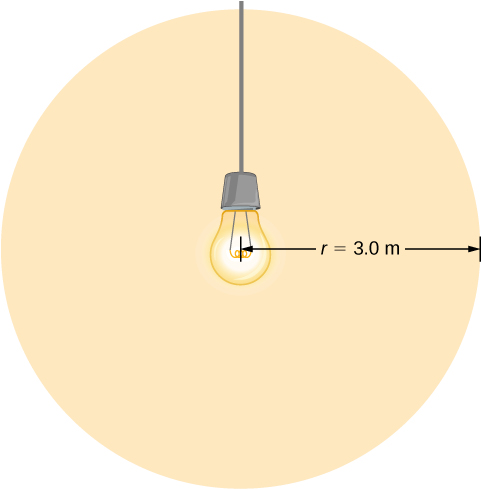
Soluzione
La potenza irradiata come luce visibile è quindi
(I = \frac{P}{4\pi r^2} = \frac{c\epsilon_0 E_0^2}{2},
(E_0 = \sqrt{2\frac{P}{4\pi r^2 c\epsilon_0}} = \sqrt{2\frac{5.00 \ W}{4\pi (3,0 \m)^2 (3,00 \volte 10^8 \m/s)(8,85 \volte 10^{-12} C^2/N \cdot m^2)}} = 5.77 \, N/C,\)
(B_0 = E_0/c = 1.92 \times 10^{-8} \, T\).
Significato
L’intensità I cade al quadrato della distanza se la radiazione è dispersa uniformemente in tutte le direzioni.
Gamma radio
Un trasmettitore radio da 60 kW sulla Terra invia il suo segnale a un satellite a 100 km di distanza (Figura \(\PageIndex{3}). A quale distanza nella stessa direzione il segnale avrebbe la stessa intensità massima di campo se la potenza di uscita del trasmettitore fosse aumentata a 90 kW?
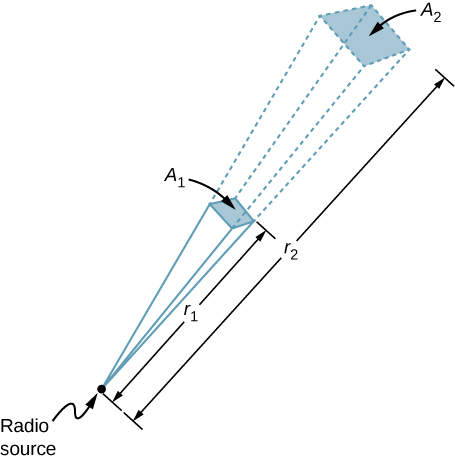
Strategia
L’area su cui si disperde la potenza in una particolare direzione aumenta al quadrato della distanza, come illustrato nella figura \(\PageIndex{3}\). Cambia la potenza in uscita P di un fattore di (90 kW/60 kW) e cambia l’area dello stesso fattore per mantenere \(I = \frac{P}{A} = \frac{c\epsilon_0 E_0^2}{2}) lo stesso. Poi usa la proporzione tra l’area A nel diagramma e la distanza al quadrato per trovare la distanza che produce il cambiamento di area calcolato.
Soluzione
Utilizzando la proporzionalità delle aree ai quadrati delle distanze, e risolvendo, otteniamo dal diagramma
\ r_2 &= \sqrt{frac{90}{60}}(100 \, km) \ &= 122 \, km. \end{align*}}]
Significato
La portata di un segnale radio è la distanza massima tra il trasmettitore e il ricevitore che permette un funzionamento normale. In assenza di complicazioni come le riflessioni da ostacoli, l’intensità segue una legge dell’inverso del quadrato, e raddoppiare la portata richiederebbe di moltiplicare la potenza per quattro.
Contributori e attribuzioni
-
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), e Bill Moebs con molti autori che hanno contribuito. Questo lavoro è concesso in licenza da OpenStax University Physics sotto una licenza Creative Commons Attribution License (by 4.0).