学習目標
このセクションの終わりには、次のことができるようになります。
- 電磁波の時間平均エネルギー密度を電場と磁場の振幅で表す
- ポインティングベクトルと電磁波のエネルギー強度を計算する
- 電磁波のエネルギーがその振幅に依存し、一方光子のエネルギーはその周波数に比例することを説明する
電子レンジを使っていた人は誰もが電磁波にエネルギーがあることを知っているはずです。 このエネルギーは、夏の太陽の暖かさのように、明白であることもあります。
電磁波は、その電場と磁場により、システムにエネルギーをもたらします。
電磁波は、その電場と磁場によってシステムにエネルギーをもたらします。これらの場は力を発揮し、システム内の電荷を動かすことができ、したがって、それに対して仕事をすることができるのです。 しかし、吸収されるかどうかにかかわらず、電磁波自体にはエネルギーがあります。 一度作られた場は、エネルギーを発生源から運び去ります。
明らかに、電場と磁場の強さが大きければ大きいほど、より多くの仕事をすることができ、電磁波が運ぶエネルギーは大きくなります。 電磁波では、電界と磁界の強さの最大値を振幅といいます(図(˶‾᷄ -̫ ‾᷅˵) )。
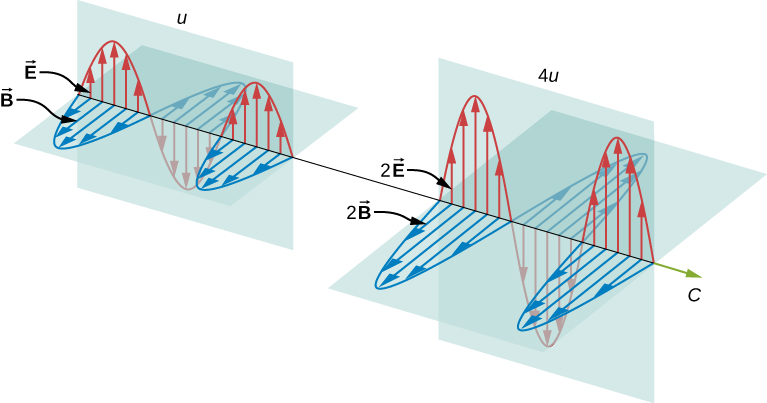
正のx軸方向に進む平面波で、波の位相が原点で最大となるように選んだ場合、電場と磁場は以下の方程式に従います
電磁波の任意の部分のエネルギーは電場と磁場のエネルギーを合計したものであります。 この単位体積あたりのエネルギー、すなわちエネルギー密度uは、電場からのエネルギー密度と磁場からのエネルギー密度の和である。 両者のエネルギー密度の式は先に述べたとおりである(キャパシタンスの場合は \(u_E**) 、インダクタンスの場合は \(u_B**) )。 これらの寄与を組み合わせると
式から、一般に電界を変化させても小さな磁界しか発生しないにもかかわらず、磁気エネルギー密度Ⓐ(u_B3↩)と電気エネルギー密度Ⓑ(u_E3↩)は等しいことがわかります。 電場と磁場のエネルギー密度が等しいということは
エネルギー密度は波と同じように電場や磁場とともに移動します。
エネルギーの移動速度は、小さな時間間隔を考えることによって求めることができます。
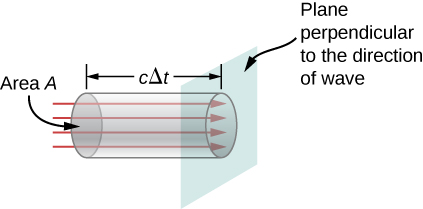

The energy passing through area \(A} in time \(\Delta t)は
The energy per unit area per unit time passing through a plane per perpendicular to the wave.つまり、単位時間あたりに、波に垂直な面を通過するエネルギーです。 エネルギーフラックスと呼ばれるエネルギーは、面積(A)と時間間隔(D)で割ることで算出されま す。
より一般的には、任意の表面を通るエネルギーのフラックスは、表面の向きにも依存する。 その方向を考慮するために、ポインティングベクトルと呼ばれるベクトル(vec{S})を導入し、以下のように定義しています。 このように、波が伝播する方向が負の方向でないことを確認するために、図16.3.2に戻りましょう。 Lenzの法則とFaradayの法則から、磁場が時間的に増加する場合、電場は(x)の方が(x + \Delta x)より大きくなることがわかります。 電界は、与えられた時間と場所において、(x)の増加とともに減少する。 電場と磁場の比例関係から、電場は磁場とともに時間的に増加することが必要である。 これは波が図の右方向に伝搬している場合のみ可能で、その場合、相対的な向きから、特に電磁波の伝搬方向において♪ \vec{S} = \frac{1}{mu_0} \times \vec{E} )が示されます。
任意の場所でのエネルギー束も、式16.3.19からⒶを式に代入するとわかるように、時間的に変化する
可視光の周波数はHzのオーダーと非常に高いので、可視光が任意の場所を通るエネルギー束は非常に速く変化する量である。 私たちの目を含む多くの計測器では、多くの周期の平均値しか検出できない。 このエネルギー束の時間平均が電磁波の強度(I)であり、単位面積当たりの電力である。 のコサイン関数を平均化することで表すことができる。29}の余弦関数を1周間平均することで表すことができ、これは何周間も時間平均することと同じです(ここでは、˶′ᴗ‵˶を1周期としています)。
積分を評価するか、あるいはサインとコサインは位相が違うだけなので1周期の平均を取れば、 \(cos^2 \, (\xi)\) も同じになり、
= \frac{1}{2} が得られます。 \langle 1 \rangle = \frac{1}{2}.\]
ここで、角括弧のⒶは時間平均の演算を表しています。 真空中を速度㎤で進む光の強度は、最大電界強度㎤(E_0)で表され、これが電界振幅でもある。 代数的な操作により、関係
ここで、 \(B_0
) は磁界振幅であり、これは最大磁界強度と同じである。 もう一つ、電界と磁界の強さを表す式が便利である。 を代入すると、先ほどの式は
3つの式は同じ結果の異なるバージョンに過ぎないので、どれが一番使いやすいかを選べばよいのです。 波のエネルギーは振幅の2乗に関係します。 さらに、これらの式は電磁波が正弦波であるという仮定に基づいているので、ピーク強度は平均強度の2倍、つまり \(I_0 = 2I) となります。 A Laser Beam
実験用の小型レーザーのビームは、通常、約 \(1.0 \times 10^{-3} W/m^2}) の強度があります。
ビームが平面波で構成されていると仮定して、ビームの電場と磁場の振幅を計算する。
強度を電場で表現する式を用いて、強度から電場を計算する。
解答
式より、レーザービームの強度は
したがって、電界の振幅は
&= \sqrt{themefrac{2}{(3.), (3.), (4.), (5.), (6.), (6.), (7.), (8.), (9.), (10.) となり、このうち強度が電界の振幅を上回ると、電界が振幅を上回ります。00 \times 10^8 m/s)(8.85 \times 10^{-12} F/m)}left(1.0 \times 10^{-3} W/m^2 \right)} ←クリックすると拡大します。 &= 0.87 \, V/m. \end{align*}}
磁界の振幅は次の式で求めることができます:
Light Bulb Fields
電球は5.00Wの電力を可視光として放射しています。
電球の出力 P が半径 3.0 m の球に一様に分布していると仮定して、強度を計算し、そこから電場を求めます。
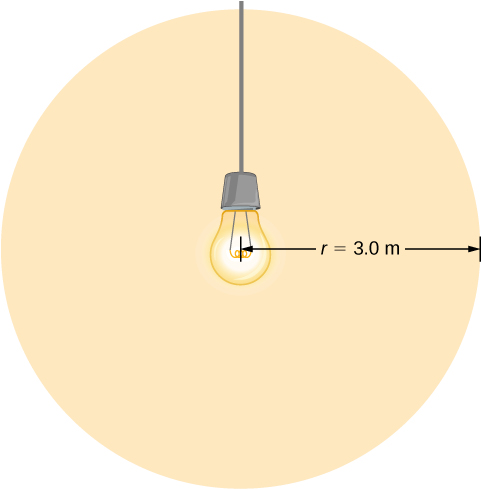
解答
可視光として放射される電力は
(I = \frac{P}{4pi r^2} = \frac{cepsilon_0 E_0^2}{2},\♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪(E_0 = \sqrt{2frac{P}{4pha r^2 cepsilon_0}} = \sqrt{2frac{5.00 \, W}{4π (3.0 \, m)^2 (3.00 \times 10^8 \, m/s)(8.85 \times 10^{-12} C^2/N \cdot m^2)}} = 5.77 \, N/C,\)
(B_0 = E_0/c = 1.92 \times 10^{-8} \, T).
意義
全方向に均一に分散させた場合、強度Iは距離の二乗で低下する。
電波の届く範囲
地球上の60kWの電波発信機が100km先の衛星に信号を送っています(図(㊦))。
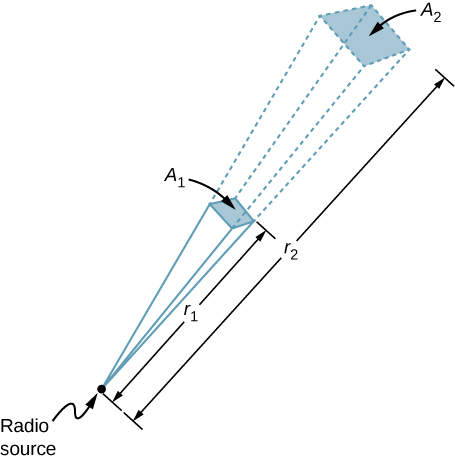
Strategy
ある方向の電力が分散される面積は、図のように距離の2乗に従って大きくなっていきます。 出力Pを(90kW/60kW)倍に変更し、面積も同じ倍数だけ変更することでⒶ(I = \frac{P}{A} = \frac{cepsilon_0 E_0^2}{2}) が同じになるようにします。 そして、図の面積Aと距離の2乗の比から、計算で求めた面積の変化をもたらす距離を求めます。
解答
距離の2乗と面積の比例を利用して解くと、図から
r_2 &= \sqrt{frac{90}{60}}(100 \, km) &= 122 \, kmとなる。
意義
無線信号の到達距離とは、送信機と受信機が正常に動作できる最大距離のことです。 障害物による反射などの複雑な要因がない場合、強度は逆二乗則に従うので、範囲を 2 倍にするには電力を 4 倍にする必要があります
貢献者と帰属
-
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University) and Bill Moebs と多くの貢献者。 この作品は、クリエイティブ・コモンズ 表示ライセンス (by 4.0) の下、OpenStax University Physicsによってライセンスされています。