Golfsnelheid op een gespannen snaar
Om te zien hoe de snelheid van een golf op een snaar afhangt van de spanning en de lineaire dichtheid, beschouw je een puls die langs een gespannen snaar wordt gestuurd (figuur \PageIndex{1}). Wanneer de gespannen snaar in rust is in de evenwichtsstand, is de spanning in de snaar constant. Beschouw een klein element van de snaar met een massa gelijk aan \(\Delta m = \mu \Delta x\). Het massa-element is in rust en in evenwicht en de spankracht aan weerszijden van het massa-element is gelijk en tegengesteld.
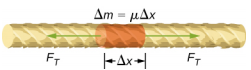
Als je aan een gespannen snaar trekt, beweegt een dwarsgolf in de positieve x-richting, zoals te zien is in figuur \(\PageIndex{2}\). Het massa-element is klein, maar is in de figuur vergroot om het zichtbaar te maken. Het kleine massa-element oscilleert loodrecht op de golfbeweging als gevolg van de door de snaar geleverde herstelkracht en beweegt niet in de x-richting. De spanning FT in de snaar, die in de positieve en negatieve x-richting werkt, is ongeveer constant en is onafhankelijk van positie en tijd.
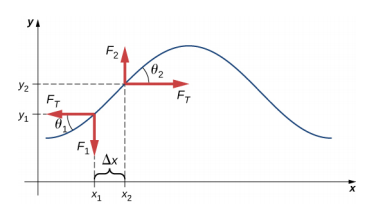
Aanname dat de helling van de verplaatste snaar ten opzichte van de horizontale as klein is. De netto kracht op het element van de snaar, dat evenwijdig aan de snaar werkt, is de som van de spanning in de snaar en de restkracht. De x-componenten van de spankracht heffen elkaar op, zodat de nettokracht gelijk is aan de som van de y-componenten van de kracht. De grootte van de x-component van de kracht is gelijk aan de horizontale spankracht van de snaar zoals weergegeven in figuur \(F_T). Om de y-componenten van de kracht te verkrijgen, moet men opmerken dat tan \theta_{1} = – \frac{F_{1}}{F_{T}}) en \tan \theta_{2} = \frac{F_{2}}{F_{T}}). De \(\tan \theta}) is gelijk aan de helling van een functie in een punt, die gelijk is aan de partiële afgeleide van y ten opzichte van x in dat punt. Daarom is \(\frac{F_{1}}{F_{T}}) gelijk aan de negatieve helling van de snaar bij x1 en \(\frac{F_{2}}{F_{T}}) is gelijk aan de helling van de snaar bij x2:
De netto kracht op het kleine massa-element kan worden geschreven als
Met behulp van de tweede wet van Newton is de netto kracht gelijk aan de massa maal de versnelling. De lineaire dichtheid van de snaar µ is de massa per lengte van de snaar, en de massa van het deel van de snaar is \(\mu \Delta)x,
Delta ma = \mu \Delta x \left(\frac{\2} y}{\partiële t^{2}} rechts) \ldotp]
Deel door FT(\Delta\)x en neem de limiet als \(\Delta\)x naar nul gaat,
Delta x} & = \frac{\mu}{F_{T}} \frac{\partieel^{2} y}{\partieel t^{2}} \frac{\partieel^{2} y}{\partieel x^{2}} & = \frac{\mu}{F_{T}} \frac{\partieel^{2} y}{\partieel t^{2}}
Denk eraan dat de lineaire golfvergelijking is
Daarom,
Oplossen voor \(v\), zien we dat de snelheid van de golf op een snaar afhangt van de spanning en de lineaire dichtheid
Snelheid van een golf op een snaar onder spanning
De snelheid van een puls of golf op een snaar onder spanning kan worden gevonden met de vergelijking
waarbij \(F_T\) de spanning in de snaar is en \(µ\) de massa per lengte van de snaar is.
Op een zessnarige gitaar heeft de hoge E-snaar een lineaire dichtheid van \(\mu_{Hoog; E}) = 3,09 x 10-4 kg/m en de lage E-snaar een lineaire dichtheid van \(\mu_{Laag; E}) = 5,78 x 10-3 kg/m. (a) Als de hoge E-snaar wordt aangeslagen, waardoor een golf in de snaar ontstaat, wat is dan de snelheid van de golf als de spanning van de snaar 56,40 N is? (b) De lineaire dichtheid van de lage E-snaar is ongeveer 20 keer zo groot als die van de hoge E-snaar. Zou de spanning van de lage E-snaar groter of kleiner moeten zijn dan die van de hoge E-snaar om golven met dezelfde golfsnelheid door de lage E-snaar te laten gaan als de hoge E-snaar? Wat zou bij benadering de spanning zijn? (c) Bereken de spanning van de lage E snaar die nodig is voor dezelfde golfsnelheid.
Strategie
- De snelheid van de golf kan worden gevonden uit de lineaire dichtheid en de spanning \(v = \sqrt{\frac{F_{T}}{\mu}}).
- Uit de vergelijking v = \(\sqrt{\frac{F_{T}}{\mu}}) volgt dat als de lineaire dichtheid met bijna een factor 20 wordt verhoogd, de spanning met een factor 20 zou moeten worden verhoogd.
- Ken we de snelheid en de lineaire dichtheid, dan kan de snelheidsvergelijking worden opgelost voor de spankracht FT = \(\mu)v2.
Oplossing
- Gebruik de snelheidsvergelijking om de snelheid te vinden: $$v = \sqrt{\frac{F_{T}}}{\sqrt{\frac{56.40; N}{3,09 \ maal 10^{-4}kg/m}} = 427,23; m/s \ldotp$$
- De spanning moet met ongeveer een factor 20 worden verhoogd. De spanning zou iets minder dan 1128 N zijn.
- Gebruik de snelheidsvergelijking om de werkelijke spanning te vinden: $$F_{T} = \ v^{2} = (5,78 \tmaal 10^{-3}kg/m)(427,23 m/s)^{2} = 1055,00 N \ldotp$$
- Deze oplossing ligt binnen 7% van de benadering.
Betekenis
De standaardnoten van de zessnarige snaar (hoge E, B, G, D, A, lage E) zijn zo gestemd dat ze trillen op de fundamentele frequenties (329,63 Hz, 246,94 Hz, 196,00 Hz, 146,83 Hz, 110,00 Hz, en 82,41 Hz) als ze worden aangeslagen. De frequenties zijn afhankelijk van de snelheid van de golven op de snaar en de golflengte van de golven. De zes snaren hebben verschillende lineaire dichtheden en worden “gestemd” door de spanning in de snaren te veranderen. We zullen in Interferentie van golven zien dat de golflengte afhangt van de lengte van de snaren en de randvoorwaarden. Om andere tonen dan de grondtonen te spelen, worden de lengtes van de snaren veranderd door de snaren naar beneden te drukken.
Oefening 16.5
De golfsnelheid van een golf op een snaar hangt af van de spanning en de lineaire massadichtheid. Als de spanning wordt verdubbeld, wat gebeurt er dan met de snelheid van de golven op de snaar?