Wave Speed on a String under Tension
Aby zobaczyć, jak prędkość fali na strunie zależy od napięcia i gęstości liniowej, rozważmy impuls wysyłany w dół napiętej struny (rysunek \). Gdy napięta struna znajduje się w spoczynku w położeniu równowagi, napięcie w strunie \(F_T\) jest stałe. Rozważmy mały element struny o masie równej \(\Delta m = \mu \Delta x \). Element masowy znajduje się w spoczynku i w równowadze, a siła napięcia po obu stronach elementu masowego jest równa i przeciwna.
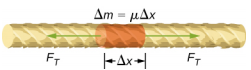
Jeśli szarpniemy strunę pod napięciem, to fala poprzeczna porusza się w dodatnim kierunku x, jak pokazano na rysunku \(\PageIndex{2}). Element masowy jest mały, ale został powiększony na rysunku, aby go uwidocznić. Mały element masowy drga prostopadle do ruchu fali w wyniku działania siły przywracającej dostarczanej przez strunę i nie porusza się w kierunku x. Napięcie FT w strunie, które działa w dodatnim i ujemnym kierunku x, jest w przybliżeniu stałe i niezależne od położenia i czasu.
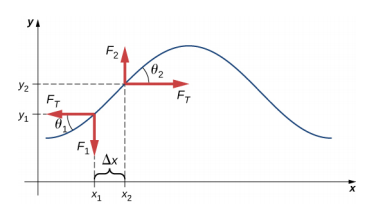
Załóżmy, że nachylenie przesuniętej struny względem osi poziomej jest małe. Siła netto działająca na element sznurka, działająca równolegle do sznurka, jest sumą napięcia w sznurku i siły przywracającej. Składowe x siły naciągu znoszą się, więc siła netto jest równa sumie składowych y tej siły. Wielkość składowej x siły jest równa poziomej sile naciągu struny (F_T), jak pokazano na rysunku. Aby otrzymać składowe y siły, należy zauważyć, że tan \(\theta_{1} = – \frac{F_{1}}{F_{T}}}) i \(\tan \theta_{2} = \frac{F_{2}}{F_{T}}}). Nachylenie funkcji w danym punkcie jest równe pochodnej cząstkowej funkcji y względem x w tym punkcie. Zatem \(\frac{F_{1}}{F_{T}}}) jest równe ujemnemu nachyleniu sznurka w punkcie x1, a \(\frac{F_{2}}{F_{T}}}) jest równe nachyleniu sznurka w punkcie x2:
Siłę netto działającą na element o małej masie można zapisać jako
Wykorzystując drugie prawo Newtona, siła netto jest równa masie razy przyspieszenie. Gęstość liniowa sznurka µ jest masą przypadającą na długość sznurka, a masa części sznurka wynosi ∗ x,
= \Delta ma = \mu \Delta x \left(\frac{partial^{2} y}{\partial t^{2}}} right) \ldotp}
Podzielenie przez FT\(\Delta\)x i przyjęcie granicy, gdy \(\Delta\)x zbliża się do zera,
}{Delta x} & = \frac{}mu}{F_{T}} \frac{partial^{2} y}{partial t^{2}} \frac{partial^{2} y}{partial x^{2}} & = \frac{partial^{} y}{F_{T}} \frac{partial^{2} y}{partial t^{2}} widzimy, że prędkość fali na strunie zależy od naprężenia i gęstości liniowej
Prędkość fali na strunie pod napięciem
Prędkość impulsu lub fali na strunie pod napięciem można znaleźć za pomocą równania
gdzie \(F_T\) jest napięciem w strunie, a \(µ\) jest masą na długość struny.
Przykład 16.5: Prędkość fali w sprężynie gitarowej
W sześciostrunowej gitarze struna o wysokim napięciu E ma gęstość liniową = 3,09 x 10-4 kg/m, a struna o niskim napięciu E ma gęstość liniową = 5,78 x 10-3 kg/m. (a) Jeśli struna o wysokim E zostanie zerwana, wytwarzając falę w strunie, to jaka jest prędkość fali, jeśli napięcie struny wynosi 56,40 N? (b) Gęstość liniowa struny niskiej E jest około 20 razy większa niż gęstość liniowa struny wysokiej E. Czy aby fale przechodziły przez strunę niskiego E z taką samą prędkością falową jak przez strunę wysokiego E, naciąg musiałby być większy czy mniejszy niż w przypadku struny wysokiego E? Jakie byłoby przybliżone naprężenie? (c) Oblicz napięcie struny niskiej E potrzebne do uzyskania tej samej prędkości fali.
Strategia
- Prędkość fali można znaleźć z gęstości liniowej i napięcia \(v = \sqrt{frac{F_{T}}{\mu}}}).
- Z równania v = \(\sqrt{frac{F_{T}}{\mu}}) wynika, że jeśli gęstość liniową zwiększymy o czynnik prawie 20, to napięcie będzie musiało wzrosnąć o czynnik 20.
- Znając prędkość i gęstość liniową, równanie prędkości można rozwiązać dla siły napięcia FT = ∗ v2.
Rozwiązanie
- Użyj równania prędkości, aby znaleźć prędkość: $$v = \sqrt{frac{F_{T}}{\mu}} = \sqrt{\frac{56.40; N}{3,09 razy 10^{-4}; kg/m}} = 427,23; m/s \dotp$$
- Naprężenie musiałoby zostać zwiększone o czynnik około 20. Naprężenie byłoby nieco mniejsze niż 1128 N.
- Użyj równania prędkości, aby znaleźć rzeczywiste naprężenie: $$F_{T} = ^mu v^{2} = (5,78 razy 10^{-3}; kg/m)(427,23; m/s)^{2} = 1055,00; N ^ldotp$$
- To rozwiązanie mieści się w 7% przybliżenia.
Znaczenie
Standardowe nuty sześciu strun (wysokie E, B, G, D, A, niskie E) są dostrojone tak, aby drgały z częstotliwościami fundamentalnymi (329,63 Hz, 246,94 Hz, 196,00 Hz, 146,83 Hz, 110,00 Hz i 82,41 Hz), gdy są szarpane. Częstotliwości zależą od prędkości fali na strunie i długości fali. Sześć strun ma różne gęstości liniowe i są one „dostrajane” poprzez zmianę napięcia w strunach. W Interferencji Fal zobaczymy, że długość fali zależy od długości strun i warunków brzegowych. Aby zagrać nuty inne niż fundamentalne, długości strun zmieniamy naciskając na nie.
Ćwiczenie 16.5
Prędkość fali na strunie zależy od napięcia i liniowej gęstości masy. Jeśli napięcie zostanie podwojone, to co się stanie z prędkością fal na strunie?