Obiective de învățare
Până la sfârșitul acestei secțiuni, veți fi capabili să:
- Exprimați densitatea de energie medie în timp a undelor electromagnetice în funcție de amplitudinile câmpurilor electrice și magnetice ale acestora
- Calculați vectorul Poynting și intensitatea energetică a undelor electromagnetice
- Explicați cum energia unei unde electromagnetice depinde de amplitudinea sa, în timp ce energia unui foton este proporțională cu frecvența sa
Cine a folosit un cuptor cu microunde știe că există energie în undele electromagnetice. Uneori, această energie este evidentă, cum ar fi în căldura Soarelui de vară. Alteori, este subtilă, cum ar fi energia nesimțită a razelor gamma, care poate distruge celulele vii.
Undele electromagnetice aduc energie într-un sistem în virtutea câmpurilor lor electrice și magnetice. Aceste câmpuri pot exercita forțe și pot deplasa sarcinile din sistem și, astfel, pot efectua un lucru asupra lor. Cu toate acestea, există energie într-o undă electromagnetică în sine, indiferent dacă este absorbită sau nu. Odată create, câmpurile transportă energia departe de o sursă. Dacă o parte din energie este absorbită ulterior, intensitatea câmpurilor este diminuată și tot ceea ce rămâne se deplasează.
Evident, cu cât intensitatea câmpurilor electrice și magnetice este mai mare, cu atât mai multă muncă pot efectua și cu atât mai mare este energia pe care o transportă unda electromagnetică. În cazul undelor electromagnetice, amplitudinea este intensitatea maximă a câmpurilor electrice și magnetice (Figura \(\PageIndex{1}\)). Energia undei este determinată de amplitudinea undei.
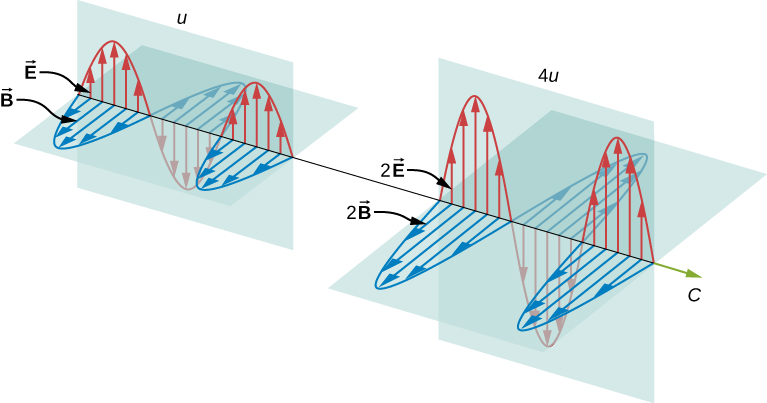
Pentru o undă plană care se deplasează pe direcția axei x pozitive, cu faza undei aleasă astfel încât maximul undei să fie la origine la \(t = 0\), câmpurile electrice și magnetice se supun ecuațiilor
Energia din orice parte a undei electromagnetice este suma energiilor câmpurilor electrice și magnetice. Această energie pe unitatea de volum, sau densitatea de energie u, este suma densității de energie din câmpul electric și a densității de energie din câmpul magnetic. Expresiile pentru ambele densități de energie de câmp au fost discutate anterior [\(u_E\) în cazul capacității și \(u_B\) în cazul inductanței]. Combinând aceste contribuții, obținem
Expresia \(E = cB = \frac{1}{\sqrt{\epsilon_0\mu_0}}B\) arată apoi că densitatea de energie magnetică \(u_B\) și densitatea de energie electrică \(u_E\) sunt egale, în ciuda faptului că modificarea câmpurilor electrice produce în general doar câmpuri magnetice mici. Egalitatea densităților de energie electrică și magnetică conduce la
Densitatea de energie se deplasează odată cu câmpurile electrice și magnetice într-un mod similar cu undele însele.
Putem afla viteza de transport a energiei luând în considerare un mic interval de timp \(\Delta t\). După cum se arată în figura \(\PageIndex{2}\), energia conținută într-un cilindru cu lungimea \(c\Delta t\) și aria secțiunii transversale A trece prin planul secțiunii transversale în intervalul \(\Delta t\).
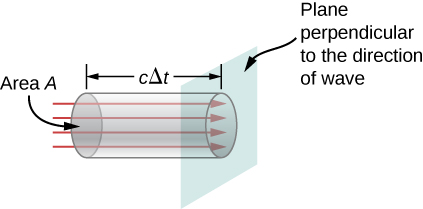
Energia care trece prin suprafața \(A\) în timpul \(\Delta t\) este
Energia pe unitatea de suprafață pe unitatea de timp care trece printr-un plan perpendicular pe undă, numită flux de energie și notată cu \(S\), poate fi calculată prin împărțirea energiei la suprafața \(A\) și la intervalul de timp \(\Delta t\).
Mai general, fluxul de energie prin orice suprafață depinde, de asemenea, de orientarea suprafeței. Pentru a lua în considerare direcția, introducem un vector \(\vec{S}\), numit vector Poynting, cu următoarea definiție:
Produsul încrucișat al lui \(\vec{E}\) și \(\vec{B}\) punctează în direcția perpendiculară la ambii vectori. Pentru a confirma că direcția lui \(\vec{S}\ este cea de propagare a undei, și nu negativul acesteia, reveniți la figura 16.3.2. Rețineți că legile lui Lenz și Faraday implică faptul că, atunci când câmpul magnetic prezentat este crescător în timp, câmpul electric este mai mare la \(x\) decât la \(x + \Delta x\). Câmpul electric scade odată cu creșterea lui \(x\) la momentul și locul date. Proporționalitatea dintre câmpurile electrice și magnetice impune ca câmpul electric să crească în timp odată cu câmpul magnetic. Acest lucru este posibil numai dacă unda se propagă spre dreapta în diagramă, caz în care, orientările relative arată că \(\vec{S} = \frac{1}{\mu_0} \vec{E} \times \vec{B}\) este în mod specific în direcția de propagare a undei electromagnetice.
Fluxul de energie în orice loc variază, de asemenea, în timp, după cum se poate observa înlocuind \(u\) din Ecuația 16.3.19 în Ecuația \ref{16.27}.
Pentru că frecvența luminii vizibile este foarte mare, de ordinul \(10^{14} \, Hz\), fluxul de energie pentru lumina vizibilă prin orice zonă este o mărime care variază extrem de rapid. Majoritatea dispozitivelor de măsurare, inclusiv ochii noștri, detectează doar o medie pe mai multe cicluri. Media în timp a fluxului de energie este intensitatea \(I\) a undei electromagnetice și reprezintă puterea pe unitatea de suprafață. Ea poate fi exprimată prin medierea funcției cosinus din ecuația \ref{16.29} pe un ciclu complet, ceea ce este același lucru cu medierea în timp pe mai multe cicluri (aici, \(T\) este o perioadă):
Putem fie să evaluăm integrala, fie să observăm că, deoarece sinusul și cosinusul diferă doar în fază, media pe un ciclu complet pentru \(cos^2 \, (\xi)\) este aceeași cu cea pentru \(sin^2 \, (\xi)\), pentru a obține
\ = \frac{1}{2} \langle 1 \rangle = \frac{1}{2}.\]
unde parantezele unghiulare \(\langle . . . \rangle \) reprezintă operația de mediere în timp. Intensitatea luminii care se deplasează cu viteza \(c\) în vid se găsește apoi a fi
în termenii intensității maxime a câmpului electric \(E_0\), care este, de asemenea, amplitudinea câmpului electric. Manipularea algebrică produce relația
unde \(B_0\) este amplitudinea câmpului magnetic, care este aceeași cu intensitatea maximă a câmpului magnetic. Este utilă încă o expresie pentru \(I_{avg}\) în termeni de intensități ale câmpului electric și magnetic. Înlocuind faptul că \(cB_0 = E_0\), expresia anterioară devine
Putem folosi oricare dintre cele trei ecuații precedente este mai convenabilă, deoarece cele trei ecuații sunt de fapt doar versiuni diferite ale aceluiași rezultat: Energia unei unde este legată de amplitudinea la pătrat. Mai mult, deoarece aceste ecuații se bazează pe ipoteza că undele electromagnetice sunt sinusoidale, intensitatea de vârf este de două ori mai mare decât intensitatea medie; adică \(I_0 = 2I\).
Exemplu \(\PageIndex{1}\): Un fascicul laser
Fasciculul de la un mic laser de laborator are de obicei o intensitate de aproximativ \(1,0 \ ori 10^{-3} W/m^2\). Presupunând că fasciculul este compus din unde plane, calculați amplitudinile câmpurilor electrice și magnetice din fascicul.
Strategie
Utilizați ecuația care exprimă intensitatea în termeni de câmp electric pentru a calcula câmpul electric din intensitate.
Soluție
Din ecuația \ref{16.31}, intensitatea fasciculului laser este
\
Amplitudinea câmpului electric este deci
\ &= \sqrt{\frac{2}{(3.00 \times 10^8 m/s)(8.85 \times 10^{-12} F/m)}\left(1.0 \times 10^{-3} W/m^2 \right)} \\ &= 0.87 \\, V/m. \end{align*}\]
Amplitudinea câmpului magnetic poate fi obținută din:
Câmpuri de becuri
Un bec emite 5,00 W de putere sub formă de lumină vizibilă. Care sunt câmpurile electrice și magnetice medii ale luminii la o distanță de 3,0 m?
Strategie
Să presupunem că puterea de ieșire P a becului este distribuită uniform pe o sferă cu raza de 3,0 m pentru a calcula intensitatea și, din aceasta, câmpul electric.
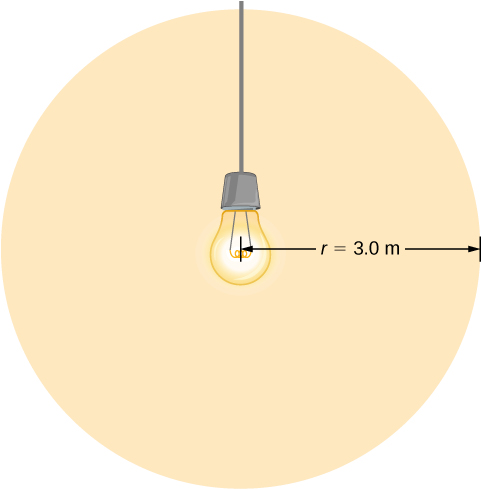
Soluție
Puterea radiată sub formă de lumină vizibilă este atunci
(I = \frac{P}{4\pi r^2} = \frac{c\epsilon_0 E_0^2}{2},\)
\(E_0 = \sqrt{2\frac{P}{4\pi r^2 c\epsilon_0}} = \sqrt{2\frac{5.00 \, W}{4\pi (3.0 \, m)^2 (3.00 \ ori 10^8 \, m/s)(8.85 \ ori 10^{-12} C^2/N \cdot m^2)}} = 5.77 \, N/C,\)
\(B_0 = E_0/c = 1,92 \times 10^{-8} \, T\).
Semnificație
Intensitatea I scade pe măsura creșterii distanței la pătrat dacă radiația este dispersată uniform în toate direcțiile.
Distanța radio
Un emițător radio de 60 kW de pe Pământ își trimite semnalul către un satelit aflat la 100 km distanță (Figura \(\PageIndex{3}\)). La ce distanță, în aceeași direcție, semnalul ar avea aceeași intensitate maximă a câmpului dacă puterea de ieșire a emițătorului ar fi crescut la 90 kW?
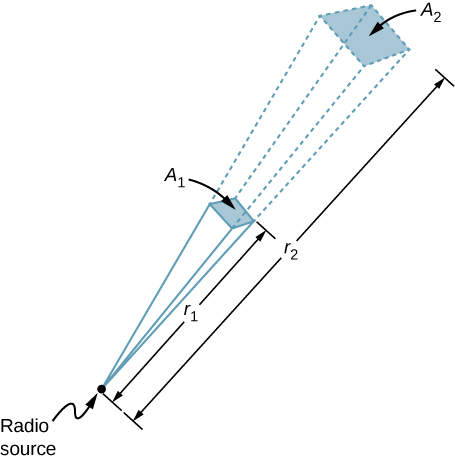
Strategie
Suprafața pe care se dispersează puterea într-o anumită direcție crește odată cu pătratul distanței, așa cum este ilustrat în figura \(\PageIndex{3}\). Modificați puterea de ieșire P cu un factor de (90 kW/60 kW) și modificați suprafața cu același factor pentru a păstra \(I = \frac{P}{A} = \frac{c\epsilon_0 E_0^2}{2}\) aceeași. Apoi folosiți proporția dintre suprafața A din diagramă și distanța la pătrat pentru a găsi distanța care produce modificarea calculată a suprafeței.
Soluție
Utilizând proporționalitatea ariilor cu pătratele distanțelor și rezolvând, obținem din diagramă
r_2 &= \sqrt{\frac{90}{60}}(100 \, km) \ &= 122 \, km. \end{align*}\}]
Semnificație
Distanța unui semnal radio este distanța maximă dintre emițător și receptor care permite o funcționare normală. În absența unor complicații, cum ar fi reflexiile de la obstacole, intensitatea urmează o lege pătratică inversă, iar dublarea razei de acțiune ar necesita înmulțirea puterii cu patru.
Contribuitori și atribuții
-
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University) și Bill Moebs cu mulți autori colaboratori. Această lucrare este licențiată de OpenStax University Physics sub licența Creative Commons Attribution License (by 4.0).
.