Användning av instrumentella variabler för att fastställa kausalitet

Fördelar med att använda instrumentella variabler för att påvisa kausalitet

Som exempel kan man tänka på frågan om att uppskatta utbildningens effekt på inkomster. Den enklaste uppskattningstekniken, vanlig minsta kvadratmetoden (OLS), genererar uppskattningar som visar att ett extra utbildningsår är förknippat med 6-10 % högre inkomster . Det positiva sambandet kan dock bero på självselektion till utbildning, dvs. att personer som har mest att vinna på mer utbildning är mer benägna att stanna kvar. Detta är t.ex. fallet om elever med högre förmåga har lättare att studera och sannolikt ändå skulle få högre löner. Den positiva korrelation som observerats mellan utbildningsår och löner skulle därför delvis avspegla bidraget på förmåga, och skulle inte kunna tolkas som avkastningen från ytterligare ett års utbildning, vilket var avsikten. OLS-skattningar skulle därför inte vara informativa om effekten av en politik som syftar till att öka antalet utbildningsår. Detta problem kallas ”omitted variable bias”. Det uppstår när en variabel (t.ex. förmåga) som inte observeras av forskaren är korrelerad både med behandlingen (mer utbildning) och med resultatet (inkomster). Riktningen (över- eller underskattning) och storleken på bias i OLS-skattningar är en funktion av korrelationernas tecken och styrka.

I det här exemplet är en randomiserad kontrollstudie (RCT), som skulle innebära att utbildning slumpmässigt tilldelas individer och att man observerar skillnaderna i deras löner under deras livstid, helt enkelt inte genomförbar av etiska skäl. Vissa naturliga eller kvasinaturliga experiment kan dock komma nära en förändring av utbildningsvalet för vissa grupper av individer och kan därför användas som instrument. Ett sådant naturligt experiment är en ändring av den lagstadgade minimiåldern för när eleverna får lämna skolan (skolavgångsåldern). Denna typ av förändring påverkar alla elever, oberoende av deras förmåga. Den fungerar därför som en yttre chock som inte kan påverkas av den enskilde eleven.

Flera länder har lagstiftning som fastställer den ålder vid vilken elever får lämna utbildningssystemet. Säg till exempel att ett barn kan lämna skolan på skolårets sista dag om det är 14 år i slutet av augusti. Låt oss nu anta att lagstiftningen ändras så att barn måste vara 15 år i slutet av augusti för att få lämna skolan. Barn som ville sluta skolan vid 14 års ålder hindras från att göra det och måste stanna kvar i ytterligare ett skolår. Under det (starka) antagandet att barn som omfattas av de två lagstiftningarna är likadana och möter liknande villkor på arbetsmarknaden, skapar lagändringen ett kvasivetenskapligt experiment: oberoende av deras förmåga kommer vissa individer att påverkas av ändringen av skolavgångsåldern och tvingas stanna kvar ytterligare ett år i skolan, medan elever med liknande preferenser från den tidigare kohorten inte kommer att göra det. Om forskarna visste vilka som ville lämna skolan vid 14 års ålder skulle de kunna jämföra resultaten för personer som lämnade skolan vid 14 års ålder med resultaten för personer som tvingades stanna kvar till 15 års ålder. Denna enkla skillnad skulle då vara den kausala effekten av att stanna kvar i skolan mellan 14 och 15 års ålder. Tyvärr gör observationsdata det inte möjligt att identifiera individer vars val av utbildning påverkades av reformen, så enligt den nya lagstiftningen kan individer som ville lämna skolan vid 15 års ålder inte särskiljas från dem som ville lämna skolan vid 14 års ålder men var tvungna att stanna kvar i ytterligare ett år. Reformen ändrar dock sannolikheten för att stanna kvar i skolan och kan därför användas som ett instrument eftersom den påverkar sannolikheten för behandling (ytterligare ett år i skolan) utan att påverka det intressanta utfallet (t.ex. inkomster).

1947 höjdes minimiåldern för skolavslutning från 14 till 15 år genom en lagändring i Storbritannien, vilket påverkade barn födda 1933 och senare. Denna lagändring ger en möjlighet att utvärdera effekten av (ytterligare) skolgång på inkomsterna. I figur 1 visar panel A att reformen påverkade både andelen barn som lämnade skolan så tidigt som möjligt (vänstra diagrammet) och den totala mängden avslutad skolgång (högra diagrammet). Skattningarna visar att reformen ökade det genomsnittliga antalet skolår för män med 0,397 år. Denna uppskattning av reformens effekt (IV) på behandlingen (utbildning) kallas ”regression i första steget”. Om utbildning har någon kausal effekt på lönen bör vi observera att den genomsnittliga lönen för individer som påverkas av reformen också är högre. Detta är verkligen fallet, vilket framgår av panel B i figur 1, där den genomsnittliga logaritmiska lönen för män redovisas. Denna serie visar ett tydligt avbrott 1933, vars storlek innebär att individer som påverkas av reformen i genomsnitt tjänar 1,2 % högre löner. Denna andra skattning av reformens effekt (IV) på utfallet (lönen) kallas ”skattning i reducerad form”. En enkel IV-strategi, som i detta fall använder ett binärt instrument som endast antar två värden (1 för att påverkas av reformen och 0 för att inte påverkas av reformen), är förhållandet mellan skattningen i reducerad form och skattningen i det första steget. (I det här fallet skulle den kausala effekten av ytterligare utbildning på inkomsterna vara 0,012/0,397 = 0,030 och därmed cirka 3 %.

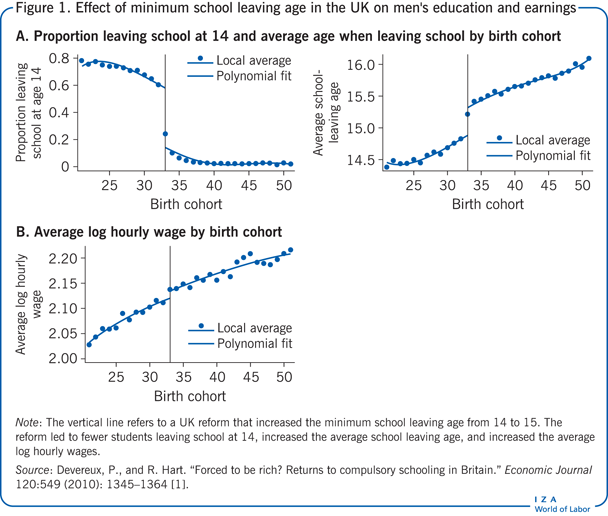
Intuitionen med detta tillvägagångssätt är att effekten av ytterligare ett års utbildning på lönen i princip är reformens (IV) effekt på lönen (utfallet)-vilket ges i reducerad form-skalerad uppåt med den effekt som reformen har på antalet utbildningsår (behandlingen)-vilket är vad skattningen i första steget handlar om. Om instrumentet är ”relevant”, dvs. har en effekt på utbildning (behandlingen), och om instrumentet påverkar lönerna ”uteslutande” genom sin effekt på utbildning, kan IV-skattningarna tolkas som behandlingens kausala effekt på utfallet. Dessa två villkor kallas ”instrumentrelevans” och ”uteslutningsbegränsning”.

För att sammanfatta, när en icke-observerad variabel som förmåga korrelerar både med behandlingen och utfallet, kommer en enkel skattning som OLS att vara snedvriden på grund av självselektion till behandlingen. På samma sätt, om behandlingsvariabeln mäts med fel, kommer OLS-uppskattningen att vara snedvriden mot noll. Det går dock att få fram en kausal uppskattning av hur behandlingen påverkar resultatet om man kan hitta ett trovärdigt instrument. Ett trovärdigt instrument måste uppfylla två villkor:

• Relevans: instrumentet måste påverka sannolikheten för behandling. I en regression av behandlingen på instrumentet, även kallad första stadiets ekvation, måste koefficienten för IV vara tillräckligt stark.

• Exklusionsrestriktion: instrumentet påverkar utfallet uteslutande via sin effekt på behandlingen.

Om ett sådant IV kan hittas (dvs.

I det föregående exemplet presenterades Wald-skattningen, dvs. förhållandet mellan skattningarna från två regressioner: skattningen i reducerad form, som kommer från en regression av utfallet på instrumentet, och skattningen i det första steget, som kommer från en regression av behandlingen på instrumentet. Detta kan lätt beräknas när instrumentet endast har två värden. I det mer allmänna fallet beräknas en s.k. 2SLS-skattning (two stage least squares), varvid förutsägelser av behandlingen från ekvationen i det första steget används i en regression av utfallet på behandlingen i stället för det verkliga värdet av behandlingen. Det är alltså endast den variation i behandlingen som kommer från instrumentet som används för att förklara variansen i resultatet. Detta löser självvalsstörningen. När det gäller ett binärt instrument (med två värden) kommer Wald- och 2SLS-skattningarna att vara identiska (se t.ex.) Svårigheten ligger dock inte i genomförandet av en sådan 2SLS-skattning, alla statistikpaket kan beräkna IV-skattningar, utan i a) att hitta ett giltigt instrument och b) att tolka resultaten. Diskussionen kommer nu att fokusera på dessa två punkter.