Tillbaka till lektionsindexet | Gör lektionerna i ordning | Utskriftsvänlig sida
Faktorsatsen
Faktorsatsen är ett resultat av restsatsen och bygger på samma resonemang. Om du inte har läst lektionen om restsatsen, gå igenom det ämnet först och återvänd sedan hit.
Som restsatsen påpekar, om du dividerar ett polynom p(x) med en faktor x – a av det polynomet, så får du en nollrester. Låt oss återigen titta på det där uttrycket för divisionsalgoritmen för polynomet:
Respekt
- (x) = (x – a)q(x) + r(x)
Om x – a verkligen är en faktor till p(x), så blir återstoden efter divisionen med x – a noll. Det vill säga:
- (x) = (x – a)q(x)
I termer av restsatsen innebär detta att om x – a är en faktor av p(x), så kommer återstoden, när vi gör en syntetisk division med
x = a, att vara noll.
Punkten med faktorsatsen är det omvända av restsatsen: Om vi syntetiskt dividerar ett polynom med x = a och får en nollrest, så är inte bara x = a en nolla i polynomet (tack vare restsatsen), utan x – a är också en faktor i polynomet (tack vare faktorsatsen).
Samma som med restsatsen är poängen här inte att göra den långa divisionen av ett givet polynom med en given faktor. Den här teoremet upprepar inte det du redan vet, utan försöker istället göra ditt liv enklare. När du ställs inför en övning i Faktorsatsen kommer du att tillämpa syntetisk division och sedan kontrollera om resten är noll.
- Använd faktorsatsen för att avgöra om x – 1 är en faktor till
f (x) = 2×4 + 3×2 – 5x + 7.
För att x – 1 ska vara en faktor till f (x) = 2×4 + 3×2 – 5x + 7 säger faktorsatsen att x = 1 måste vara en nolla till f (x). För att testa om x – 1 är en faktor kommer jag först att sätta x – 1 lika med noll och lösa för att hitta den föreslagna nollpunkten, x = 1. Sedan kommer jag att använda syntetisk division för att dividera f (x) med x = 1. Eftersom det inte finns någon kubisk term kommer jag att vara noga med att komma ihåg att sätta in en ”0” på den första raden i den syntetiska divisionen för att representera den utelämnade potensen av x i 2×4 + 3×2 – 5x + 7:
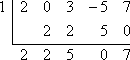
Då återstoden inte är noll, säger faktorsatsen att:
x – 1 är inte en faktor till f (x).
- Varmed hjälp av faktorsatsen kan du verifiera att x + 4 är en faktor till
f (x) = 5×4 + 16×3 – 15×2 + 8x + 16.
Om x + 4 är en faktor, då (genom att sätta denna faktor lika med noll och lösa) x = -4 är en rot. För att göra den nödvändiga verifieringen måste jag kontrollera att när jag använder syntetisk division på f (x), med x = -4, får jag en rest på noll:
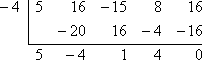
Resten är noll, så faktorsatsen säger att:
x + 4 är en faktor till 5×4 + 16×3 – 15×2 + 8x + 16.
I praktiken används faktorsatsen när man faktoriserar polynom ”fullständigt”. Istället för att pröva olika faktorer med hjälp av lång division använder man syntetisk division och Faktorsatsen. Varje gång du dividerar med ett tal (som är en potentiell rot i polynomet) och får en nollrest i den syntetiska divisionen betyder det att talet verkligen är en rot, och därmed är ”x minus talet” en faktor. Då fortsätter du divisionen med det resulterande mindre polynomet, och fortsätter tills du kommer fram till en linjär faktor (så att du har hittat alla faktorer) eller en kvadratisk (på vilken du kan tillämpa den kvadratiska formeln).
- Med hjälp av det faktum att -2 och 1/3 är nollställen till f (x) = 3×4 + 5×3 + x2 + 5x – 2, faktoriserar du polynomet fullständigt. Copyright © Elizabeth Stapel 2002-2011 Alla rättigheter förbehållna
Om x = -2 är en nolla så är x + 2 = 0, så x + 2 är en faktor. På samma sätt, om x = 1/3 är en nolla, så är x – 1/3 = 0, så x – 1/3 är en faktor. Genom att ge mig två nollor har de också gett mig två faktorer: Eftersom jag började med ett polynom av fjärde graden kommer jag att få en kvadratisk faktor när jag har delat ut dessa två givna faktorer. Jag kan lösa den kvadratiska genom att använda den kvadratiska formeln eller någon annan metod.
Faktorsatsen säger att jag inte behöver göra den långa divisionen med de kända faktorerna x + 2 och x – 1/3. I stället kan jag använda syntetisk division med de tillhörande nollorna -2 och 1/3. Här är vad jag får när jag gör den första divisionen med x = -2:
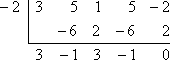
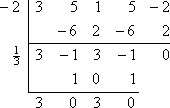
Detta lämnar mig med kvadraten 3×2 + 3, som jag kan lösa:
3×2 + 3 = 0
3(x2 + 1) = 0
x2 + 1 = 0
x2 = -1
x = ± i
Om nollpunkterna är x = -i och x = i, så är faktorerna x – (-i) och x – (i), eller x + i och x – i. I need to remember that I divided off a ”3” when I solved the quadratic; it is still part of the polynomial, and needs to be included as a factor. Then the fully-factored form is:
3×4 + 5×3 + x2 + 5x – 2 = 3(x + 2)(x – 1/3)(x + i)(x – i)
Top | Return to Index
|
Cite this article as: |
Stapel, Elizabeth. ”The Factor Theorem.” Purplemath. Available from 2016
|