ISLAMISK MATEMATIK

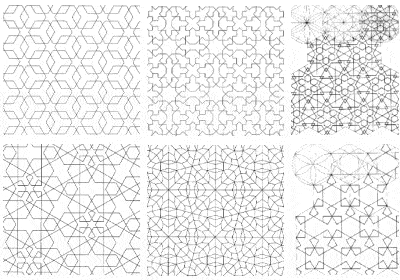
Några exempel på komplexa symmetrier som används i islamisk tempeldekoration

Det islamiska riket som etablerades i Persien, Mellanöstern, Centralasien, Nordafrika, Iberiska halvön och delar av Indien från och med 800-talet bidrog i hög grad till matematiken. De kunde dra nytta av och smälta samman den matematiska utvecklingen i både Grekland och Indien.

En konsekvens av det islamiska förbudet mot att avbilda den mänskliga formen var den omfattande användningen av komplexa geometriska mönster för att dekorera deras byggnader, vilket höjde matematiken till en konstform. Med tiden upptäckte muslimska konstnärer faktiskt alla de olika former av symmetri som kan avbildas på en tvådimensionell yta.

Kvianen i sig uppmuntrade till kunskapsinsamling, och en guldålder för islamisk vetenskap och matematik blomstrade under hela den medeltida perioden från 800-talet till 1400-talet. Vishetens hus inrättades i Bagdad omkring 810, och arbetet med att översätta de viktigaste grekiska och indiska matematiska och astronomiska verken till arabiska påbörjades nästan omedelbart.

Den enastående persiska matematikern Muhammad Al-Khwarizmi var en av de tidiga direktörerna för Vishetens hus på 800-talet, och en av de största av de tidiga muslimska matematikerna. Al-Khwarizmis kanske viktigaste bidrag till matematiken var hans starka förespråkande av det hinduiska numeriska systemet (1 – 9 och 0), som han insåg hade den kraft och effektivitet som krävdes för att revolutionera den islamiska (och senare även den västerländska) matematiken, och som snart antogs av hela den islamiska världen, och senare även av Europa.

Al-Khwarizmis andra viktiga bidrag var algebra, och han introducerade de grundläggande algebraiska metoderna ”reduktion” och ”balansering” och gav en uttömmande redogörelse för hur man löser polynomiska ekvationer upp till andra graden. På detta sätt bidrog han till att skapa det kraftfulla abstrakta matematiska språk som fortfarande används över hela världen i dag, och möjliggjorde ett mycket mer generellt sätt att analysera andra problem än bara de specifika problem som tidigare betraktades av indierna och kineserna.

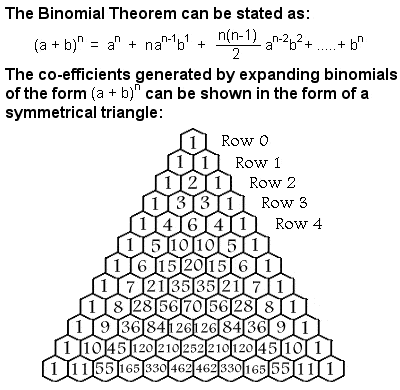
Binomialsatsen

Den persiske matematikern Muhammad Al-Karaji på 900-talet arbetade för att utvidga algebran ännu mer, frigöra den från sitt geometriska arv, och introducerade teorin om algebraisk kalkyl. Al-Karaji var den förste som använde metoden bevis genom matematisk induktion för att bevisa sina resultat, genom att bevisa att det första påståendet i en oändlig sekvens av påståenden är sant, och sedan bevisa att om något av påståendena i sekvensen är sant, så är även nästa sant.

Binomialsatsen

Al-Karaji använde bland annat matematisk induktion för att bevisa binomialsatsen. Ett binom är en enkel typ av algebraiskt uttryck som bara har två termer som endast opereras med addition, subtraktion, multiplikation och positiva exponenter för hela tal, till exempel (x + y)2. De koefficienter som behövs när ett binom expanderas bildar en symmetrisk triangel, som brukar kallas Pascals triangel efter den franske 1600-talsmatematikern Blaise Pascal, även om många andra matematiker hade studerat den århundraden före honom i Indien, Persien, Kina och Italien, bland annat Al-Karaji.

Vissa hundra år efter Al-Karaji generaliserade Omar Khayyam (kanske mer känd som poet och författare av ”Rubaiyat”, men en viktig matematiker och astronom i sin egen rätt) indiska metoder för att extrahera kvadrat- och kubikrötter till att inkludera fjärde, femte och högre rötter i början av 1100-talet. Han genomförde en systematisk analys av kubiska problem och avslöjade att det faktiskt fanns flera olika sorters kubiska ekvationer. Även om han faktiskt lyckades lösa kubiska ekvationer, och även om han vanligen tillskrivs skulden för att ha identifierat grunderna för algebraisk geometri, hindrades han från ytterligare framsteg av sin oförmåga att separera algebra från geometri, och en rent algebraisk metod för lösning av kubiska ekvationer fick vänta ytterligare 500 år och de italienska matematikerna del Ferro och Tartaglia.

Sfärisk trigonometri

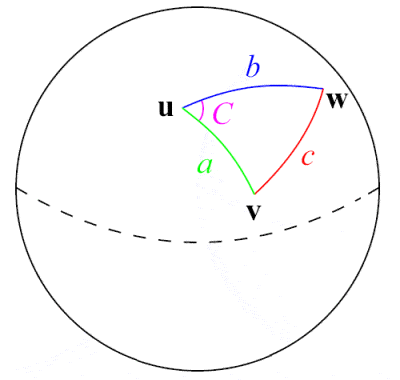
Al-Tusi var en pionjär inom området sfärisk trigonometri

Den persiske astronomen, vetenskapsmannen och matematikern Nasir Al-Din Al-Tusi från 1200-talet var kanske den första som behandlade trigonometri som en separat matematisk disciplin, skild från astronomi. Med utgångspunkt i tidigare arbeten av grekiska matematiker som Menelaos av Alexandria och indiska arbeten om sinusfunktionen gav han den första omfattande redogörelsen för sfärisk trigonometri, inklusive en förteckning över de sex olika fallen av en rätvinklig triangel i sfärisk trigonometri. Ett av hans viktigaste matematiska bidrag var formuleringen av den berömda sinuslagen för plana trianglar, a⁄(sin A) = b⁄(sin B) = c⁄(sin C), även om sinuslagen för sfäriska trianglar hade upptäckts tidigare av 900-talspersianerna Abul Wafa Buzjani och Abu Nasr Mansur.

Andra medeltida muslimska matematiker värda att notera är bland annat:

• den arabiska Thabit ibn Qurra från 800-talet, som utvecklade en allmän formel genom vilken amicabla tal kunde härledas, vilket återupptäcktes långt senare av både Fermat och Descartes (amicabla tal är par av tal för vilka summan av divisorerna till det ena talet är lika med det andra talet, e.t.ex. är de egentliga delarna av 220 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 och 110, varav summan är 284, och de egentliga delarna av 284 är 1, 2, 4, 71 och 142, varav summan är 220);
• den arabiska matematikern Abul Hasan al-Uqlidisi från 900-talet, som skrev den tidigaste bevarade texten som visar hur de arabiska siffrorna användes för att bestämma positionen, och i synnerhet hur man använde decimaltal i stället för bråk (t.ex.g. 7.375 i stället för 73⁄8);
• den arabiska geometern Ibrahim ibn Sinan från 900-talet, som fortsatte Arkimedes undersökningar av areor och volymer samt av en cirkels tangenter;
• Persern Ibn al-Haytham (även känd som Alhazen) från 1000-talet, som förutom sina banbrytande arbeten om optik och fysik, etablerade början på kopplingen mellan algebra och geometri och utformade det som nu är känt som ”Alhazens problem” (han var den förste matematikern som härledde formeln för summan av fjärde potenser, med hjälp av en metod som är lätt att generalisera); och
• trettonhundratalets perser Kamal al-Din al-Farisi, som tillämpade teorin om koniska sektioner för att lösa optiska problem, samt fortsatte sitt arbete inom talteori, t.ex. om amicabla tal, faktorisering och kombinatoriska metoder;
• den marockanske Ibn al-Banna al-Marrakushi från 1200-talet, vars arbeten omfattade ämnen som beräkning av kvadratrötter och teorin om fortsatta bråk, samt upptäckten av det första nya paret av amicabla tal sedan antiken (17 296 och 18 416, som senare återupptäcktes av Fermat) och den första användningen av algebraisk notation sedan Brahmagupta.

Med det turkiska ottomanska rikets kvävande inflytande från och med 1300- eller 1400-talet stagnerade den islamiska matematiken och vidareutvecklingen flyttades till Europa.

< < Tillbaka till Madhava

Framåt till Al-Khwarizmi >>