Det finns släktträd och populationer där principen om panmiktisk parning i princip är bruten. Vanligtvis rör det sig om geografiskt eller socialt relativt isolerade små samhällen. I dessa samhällen kan inavel, dvs. samkönad parning av olika slag (förälder – barn, syskon, kusiner, farbror – syster osv.), vara mycket utbredd.
Problemet med inavelns inflytande på befolkningen är ett viktigt problem inom genetiken 1. Nu har detta problem ännu inte fått någon slutgiltig lösning.
I de flesta fall tar inavel i ett släktträd hänsyn till tre generationer. Det är de mest avlägsna släktingarna som beaktas vid samkönade parningar finns det nästkusiner.
Insvenskheten beaktas med hjälp av inavelsfaktorn.
Inavelsfaktorn är sannolikheten för att två alleler är identiska till ursprunget.
Låt oss betrakta metoden för beräkning av inavelsfaktorn i ett släktträd som erbjuds av Wright 1, 2.
För att hitta inavelsfaktorn är det nödvändigt:
För att fastställa inavelsfaktorn måste man för de gifta ättlingarna hitta alla vägar i släktträdet som genom den gemensamma förfadern förbinder dessa ättlingar.
För att fastställa inavelsfaktorn måste man räkna upp antalet steg (generationsväxlingar) på varje väg.
Då är inavelsfaktorn lika med:
 ……(1)
……(1)
där r är antalet vägar, m1, m2, …. mi- antal steg på varje väg.
En gång till ska vi notera att antalet addender i summan (1) är lika med antalet vägar som genom de gemensamma förfäderna ansluter till giftermål.
Låt oss betrakta konkreta fall av släktträd, figur 1. I denna figur betyder kvadraten en manlig individ cirkeln – en kvinnlig individ. Streckade linjer och identiska siffror anger möjliga sätt i ett släktträd som genom den gemensamma förfadern (mannen eller kvinnan) ansluter avkomlingar konsanguina giftermål. På vissa platser med vägar, figur 1с, finns det två siffror 1 och 2. Det anger att sådana platser är gemensamma för de olika sätten.
Äktenskapet mellan far och dotter är incest, figur 1а. Den efterkommande (kvinnan) är kopplad till förfadern (mannen) där 1 väg med ett steg, dvs. m = 1. Därför finns det en inavelsfaktor.
Ft = 1/2.2-1 = 1/4
Det finns ett äktenskap mellan bror och syster (sibs), figur 1b. Siffrorna anger antalet sätt. Antalet identiska siffror på vägen från den gifta mannen till kvinnan är lika med antalet steg.
Låt varje ättling som har gift sig kopplar ihop sig med sin partner på två sätt med två steg på varje sätt, dvs. m = 2. Därför finns det en inavelfaktor.
Ft = 1/2.(2-2 + 2-2) = 1/4
Äktenskapet mellan kusiner visas på figur 1с.
Figur 1. Några typer av inavel i ett släktträd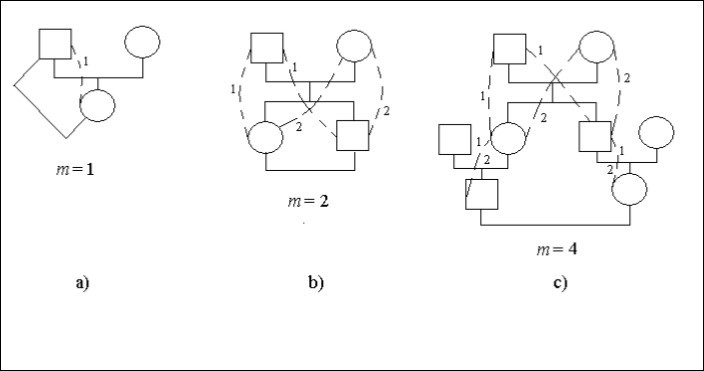
Varje ättling som har gift sig ansluter sig till partnern på 2 sätt med 4 steg på varje sätt, dvs. m = 4. Därför finns det en inavelsfaktor.
Ft = 1/2.(2-4 + 2-4) = 1/16
Formeln (1) är lätt att förstå utifrån följande logik.
Oppenbarligen finns det 1/2 gener hos barnet som är gemensamma med varje förälder, 1/4 – med morfar och mormor, 1/8 – med farfar och farfars farfar och farfars farfars farfar, osv. Om från kvinnan till någon förfader leder vägen med η steg är andelen av de gemensamma generna med denna förfader lika med 2-η. Om man från mannen till någon förfader leder vägen med μ steg är andelen av de gemensamma generna lika med 2-μ. När mannen och kvinnan gifter sig med den gemensamma förfadern kommer andelen gemensamma gener med denna förfader att vara 2-η. 2-μ = 2-m där m = η + μ är det totala antalet steg genom den gemensamma förfadern från kvinnan fram till att mannen gifter sig. Storleken 1/2 2-m visar sannolikheten för att den gen som slumpmässigt väljs hos kvinnan kommer att vara identisk till ursprunget med den gen som slumpmässigt väljs hos mannen. Samma storlek anger bidraget till inavelsfaktorn Ft en väg genom den gemensamma förfadern från kvinnan fram till att mannen gifter sig.
Till exempel, om den gemensamma förfadern kommer att vara borta från att gifta sig på η = μ = 5 generationer är sannolikheten att de har den gemensamma genen lika stor. 1/2 2-(5+5) = 1/2048 Denna storlek vid analysen av parning kan försummas. (Tabell 1)
Tabell 1.Inavelsfaktorer för vissa konsanguina äktenskap visas dessutom.
| Stypen av konsanguina äktenskap. äktenskap | Infödningsfaktor Ft |
| Sekunda kusiner | 1/32 |
| Kusinonkel – niece | 1/32 |
| Third cousins | 1/64 |
The inbreeding factor Ft is the probability of two alleles in posterity are identical by origin i.e. occur from same gene of ancestor 1. Or, that too most, the inbreeding factor is a probability of the allele origin in posterity is consanguineous. Hence, the probability of the non-consanguineous origins of identical alleles in homologous chromosomes is equal 1 – Ft.
Let’s find total probability of the recessive homozygote aa occurrence (eventаа) at random mating for an autosomal genes 3:
 …….(2)
…….(2)
This formula follows from the following logic of mating: Om ursprunget till identiska alleler i homologa autosomer inte är konsanguint (sannolikheten för denna hypotes är P(H1) = 1- Ft ) uppstår också homozygotаа (villkorad sannolikhet för denna händelse är P(aa/H1) = q2) eller om ursprunget till identiska alleler är konsanguint (sannolikheten för denna hypotes är P(H2) = Ft ) och uppstår homozygotаа (villkorad sannolikhet för denna händelse är P(aa/H2) = q). Sannolikheten q för förekomsten av homozygoten aa i det senare fallet bestäms av att om allelen a finns i en autosom bör samma allel nödvändigtvis finnas i den homologa autosomen när homozygoten har ett konsanguint ursprung.
Därmed är den totala sannolikheten för den recessiva homozygotens förekomst lika med:
 ……….(3)
……….(3)
där det tas hänsyn till p = 1 – q finns den dominanta allelen a frekvens.
På samma sätt finner man den totala sannolikheten för att den dominanta homozygoten AA förekommer vid slumpmässig parning:
 ……….. (4)
……….. (4)
Så enligt (3) och (4) ökar den totala frekvensen av homozygoter (dominanta och recessiva) i inavlade släktträd på 2Ftpq. Därför minskar frekvensen av heterozygoter för samma storlek och blir lika med 2pq – 2pqFt = 2pq(1-Ft) eftersom summan av alla zygotfrekvenser är lika med 1.
Med tanke på inavelsfaktorn och även (3) och (4) behöver Hardy-Weinberg-lagen i den följande generationen av ett inavlat släktträd för ett autosomalt genom skrivas ner fördelningarna av zygotgenotyperna som 4:
 …………(5)
…………(5)
Om pn är den dominerande allelen A frekvensen i generation n, qn – den recessiva allelen a frekvensen, så pn + qn = 1.
Kvoten (5) hänvisar också till Wrights kvot 5. Wrights kvot visar att i ett inavlat släktträd efter samkönad parning av individer observeras följande effekter: det sker en ökning av den autosomala homozygotfraktionen i ett släktträd på Ft pnqnoch en minskning av den autosomala heterozygotfraktionen i (1-F1) i jämförelse med en panmictisk population.
Men redan efter en generation återställs Hardy-Weinberg-balansen, som anger den ringa betydelsen av den separata konsanguina parningen för ett släktträd:
 ………(6)
………(6)
För en population i sin helhet kommer den separata handlingen med konsanguina parningar uppenbarligen att ha en ännu mindre betydelse än för ett släktträd.
Samma effekt av variationen i frekvensen av zygotgenotgener observeras och för könsbundna gener.
Fördelningen av de genotyper som är kopplade till Х-kromosomen i ett panmictiskt släktträd beskrivs av Hardy-Weinberg-lagen som 1:
 ………..(7)
………..(7)
Frekvensen av den dominerande allelen A ska vi ange hos männen pm och hos kvinnorna pf. För recessiva alleleresa är den följaktligen qm och qf .
Vid parning finns det ett förhållande mellan genotyperna hos kvinnorna enligt produkten (pf + qf) (pm +qm).
Låt oss hitta den totala sannolikheten för förekomsten av den recessiva homozygoten aa vid en slumpmässig parning för dotterns gener kopplade tillХ-kromosomen enligt formeln (2). Logiken för händelserna liknar fallet för autosomer förutom att den betingade sannolikheten för förekomsten av en genotypаа från de icke-konsanguina allelerna enligt (7) är lika med P(aa/H1) = qmnqfn. För de konsanguina allelerna är den betingade sannolikheten för förekomst av genotypаа lika med P(aa/H2) = qf(n+1). Vid döttrar, dvs. i generation n+1, bestäms sannolikheten för att en homozygot aa förekommer av att om allelen a finns i en Х-kromosom så bör samma allel nödvändigtvis finnas i den homologa Х-kromosomen vid homozygotens konsanguina ursprung.
Därmed är den totala sannolikheten för förekomsten av den recessiva homozygoten lika med:
 ……(8)
……(8)
där pmn är frekvensen av de dominanta allelerna A i generation n hos män och pfn – hos kvinnor. För de recessiva allelerna a följaktligen qmn och qfn . Dessutom används qmn =1 – qmn och pfn = 1 – qfn.
För att finna den totala sannolikheten för den dominanta homozygotens förekomst använder man:
 ,
,
 ……….(9)
……….(9)
och en heterozygot P(Aa) = 1- P(aa) – P(AA) ska vi finna fördelningen av genotyperna i Х-kromosomer i det inavlade släktträdet vid parning:
 ……..(10)
……..(10)
Det påvisas samtidigt att såväl som i autosomerna är de inavlade tillsatserna i dominanta och recessiva homozygotfrekvenser i de könsbundna kromosomerna identiska.
Ett annat sätt att finna förhållandet (10) kommer att bestå i följande:
Låt oss först finna den totala sannolikheten för att en heterozygot Aa förekommer, dvs. P(Aa) vid tillfället för den slumpmässiga konsanguina parningen. Denna sannolikhet följer av följande logik för parning: Allelernas ursprung är icke-konsanguint (sannolikheten för denna hypotes är P(H1) = 1 – Ft ) uppstår också heterozygot Aа (villkorad sannolikhet för denna händelse är P(Aa/H1) = pmnqfn + pfnqmn, se formel (7)) eller om allelernas ursprung är konsanguint (sannolikheten för denna hypotes är P(H2) = Ft) och det uppstår heterozygot Aа (den betingade sannolikheten för denna händelse är lika med noll P(Aa/H2) = 0 ). Det sista påståendet definieras av att vid samkönat ursprung kan liknande alleler i homologa Х-kromosomer inte leda till att heterozygoten Aa uppstår som består av olika alleler.
Därmed finner vi med hjälp av formeln för total sannolikhet den totala sannolikheten för förekomsten av heterozygoten Aa:
 ……..(11)
……..(11)
Förlust av frekvensen av heterozygot Aa sker som tidigare bevisats på grund av en identisk ökning av frekvensen av dominanta AA- och recessiva aa-homozygoter. Till exempel är ökningen av frekvensen av recessiva aa homozygoter lika:
 ……..(12)
……..(12)
Där minskningen av frekvensen av heterozygoter Aa i förhållande till det panmiktiska släktträdet enligt (7) och (11) är lika stor. ΔP(Aa) = – Ft (pmnqfn + pfnqmn) Genom att använda (11) och (12) för att uppdatera (7) för fall av inavel finner vi fördelningen av genotyper (10) i Х-kromosomer i döttrarnas inavlade släktträd.
I följande generation är frekvensen av de recessiva allelerna a hos kvinnorna lika:
 ……..(13)
……..(13)
Det stämmer helt och hållet överens med samma frekvens vid avsaknad av inavel, dvs. Hardy-Weinberg-balansen är återställd, eller mer exakt närmar sig balansen.
Kvoten (7) och (13) visar som helhet att allelfrekvenserna i ett släktträd för hänsyn till inavel inte varierar. Det sker endast en omfördelning av alleler. En del av allelerna lämnar heterozygoterna och övergår till homozygoterna.