Leerdoelen
Aan het eind van dit deel zul je in staat zijn om:
- De tijdsgemiddelde energiedichtheid van elektromagnetische golven uitdrukken in termen van hun elektrische en magnetische veldamplitude
- De Poyntingvector en de energie-intensiteit van elektromagnetische golven berekenen
- Uitleggen hoe de energie van een elektromagnetische golf afhangt van zijn amplitude, terwijl de energie van een foton evenredig is met zijn frequentie
Iedereen die wel eens een magnetron heeft gebruikt, weet dat er energie in elektromagnetische golven zit. Soms is deze energie duidelijk, zoals in de warmte van de zomerzon. Andere keren is zij subtiel, zoals de onvoelbare energie van gammastralen, die levende cellen kunnen vernietigen.
Elektromagnetische golven brengen energie in een systeem door middel van hun elektrische en magnetische velden. Deze velden kunnen krachten uitoefenen en ladingen in het systeem verplaatsen en er dus werk mee verrichten. Er zit echter energie in een elektromagnetische golf zelf, of die nu wordt geabsorbeerd of niet. Eenmaal gecreëerd, dragen de velden energie weg van een bron. Als later een deel van de energie wordt geabsorbeerd, neemt de veldsterkte af en reist alles wat overblijft verder.
Het is duidelijk dat hoe groter de sterkte van de elektrische en magnetische velden is, hoe meer werk zij kunnen verrichten en hoe groter de energie is die de elektromagnetische golf draagt. Bij elektromagnetische golven is de amplitude de maximale veldsterkte van de elektrische en magnetische velden (figuur). De golfenergie wordt bepaald door de golfamplitude.
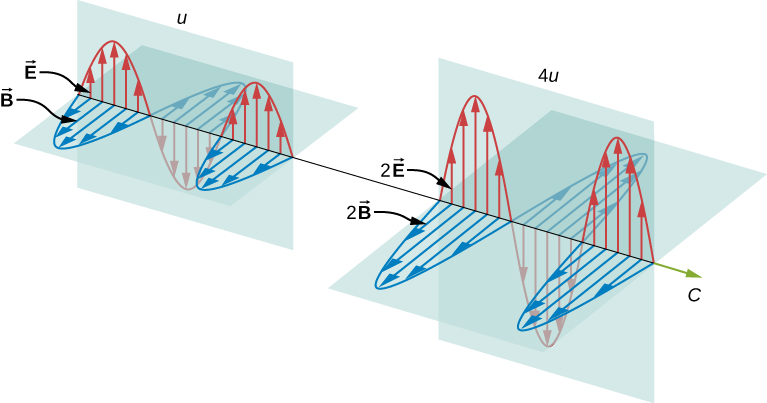
Voor een vlakke golf die in de richting van de positieve x-as beweegt en waarvan de fase van de golf zo is gekozen dat het golfmaximum bij de oorsprong ligt op t = 0, gehoorzamen de elektrische en magnetische velden aan de vergelijkingen
De energie in elk deel van de elektromagnetische golf is de som van de energieën van de elektrische en magnetische velden. Deze energie per volume-eenheid, of energiedichtheid u, is de som van de energiedichtheid van het elektrische veld en de energiedichtheid van het magnetische veld. De uitdrukkingen voor beide veld-energiedichtheden zijn eerder besproken (u_E bij Capaciteit en u_B bij Inductantie). Door deze bijdragen te combineren verkrijgen we
De uitdrukking E = cB = \frac{1}{\sqrt{\epsilon_0}}B>) laat dan zien dat de magnetische energiedichtheid \(u_B\) en de elektrische energiedichtheid \(u_E\) gelijk zijn, ondanks het feit dat veranderende elektrische velden in het algemeen slechts kleine magnetische velden produceren. De gelijkheid van de elektrische en magnetische energiedichtheden leidt tot
De energiedichtheid beweegt mee met de elektrische en magnetische velden op een vergelijkbare manier als de golven zelf.
We kunnen de snelheid van het energietransport vinden door een klein tijdsinterval \(\Delta t\) te beschouwen. Zoals in figuur
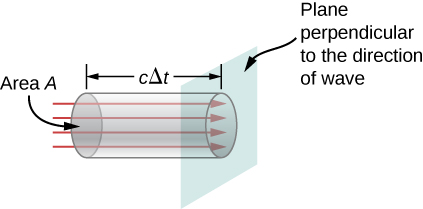

De energie die in de tijd door het gebied A gaat, wordt
De energie per oppervlakte-eenheid per tijdseenheid die door een vlak loodrecht op de golf gaat, wordt
De energie per oppervlakte-eenheid per tijdseenheid die door een vlak loodrecht op de golf gaat, wordt
De energie per oppervlakte-eenheid per tijdseenheid die door een vlak loodrecht op de golf gaat, de energieflux genoemd, kan worden berekend door de energie te delen door de oppervlakte (A) en het tijdsinterval (delta t).
Meer in het algemeen hangt de flux van energie door een oppervlak ook af van de oriëntatie van het oppervlak. Om rekening te houden met de richting introduceren we een vector (\vec{S}), de Poyntingvector genoemd, met de volgende definitie:
Het kruisproduct van \(\vec{E}) en \(\vec{B}) wijst in de richting loodrecht op beide vectoren. Om te bevestigen dat de richting van \(\vec{S}}) die van de golfvoortplanting is, en niet de negatieve, ga terug naar figuur 16.3.2. Merk op dat de wetten van Lenz en Faraday inhouden dat bij een toenemend magnetisch veld het elektrisch veld bij x groter is dan bij x + delta x). Het elektrisch veld neemt af bij toenemende \(x) op de gegeven tijd en plaats. De evenredigheid tussen elektrische en magnetische velden vereist dat het elektrische veld in de tijd toeneemt samen met het magnetische veld. Dit is alleen mogelijk als de golf zich in het diagram naar rechts voortplant, in welk geval uit de relatieve oriëntaties blijkt dat (\vec{S} = \frac{1}{\mu_0} \vec{E} \times \vec{B}) specifiek in de voortplantingsrichting van de elektromagnetische golf ligt.
De energieflux op een willekeurige plaats varieert ook in de tijd, zoals te zien is door \(u) uit vergelijking 16.3.19 te substitueren in vergelijking \ref{16.27}.
Omdat de frequentie van zichtbaar licht zeer hoog is, in de orde van \(10^{14} \, Hz), is de energieflux voor zichtbaar licht door een willekeurig gebied een extreem snel variërende grootheid. De meeste meetinstrumenten, waaronder onze ogen, nemen slechts een gemiddelde over vele cycli waar. Het tijdsgemiddelde van de energieflux is de intensiteit van de elektromagnetische golf en is het vermogen per oppervlakte-eenheid. Het kan worden uitgedrukt door het gemiddelde te nemen van de cosinusfunctie in Vergelijking 16.29} over één volledige cyclus, wat hetzelfde is als tijdgemiddelde over vele cycli (hier is \(T\) één periode):
We kunnen de integraal berekenen, of opmerken dat omdat de sinus en cosinus alleen in fase verschillen, het gemiddelde over een hele cyclus voor \(cos^2 \, (\xi)\) hetzelfde is als voor \(sin^2 \, (\xi)\), zodat we
= \frac{1}{2} \langle 1 \rangle = \frac{1}{2}.\]
waarbij de haakjes \(\langle . . . \rangle \) staan voor de tijd-gemiddelde operatie. De intensiteit van licht met een snelheid van c in vacuüm is dan
in termen van de maximale elektrische veldsterkte \(E_0), die ook de elektrische veldamplitude is. Algebraïsche manipulatie levert de relatie
waarbij \(B_0) de magnetische veldamplitude is, die hetzelfde is als de maximale magnetische veldsterkte. Nog een uitdrukking voor \(I_{avg}) in termen van zowel elektrische als magnetische veldsterktes is nuttig. Door het feit dat cB_0 = E_0 in te vullen, wordt de vorige uitdrukking
We kunnen de drie voorgaande vergelijkingen gebruiken die ons het beste uitkomen, want de drie vergelijkingen zijn eigenlijk gewoon verschillende versies van hetzelfde resultaat: De energie in een golf is gerelateerd aan de amplitude in het kwadraat. Omdat deze vergelijkingen gebaseerd zijn op de aanname dat de elektromagnetische golven sinusvormig zijn, is bovendien de piekintensiteit twee keer zo groot als de gemiddelde intensiteit; dat wil zeggen: I_0 = 2I_).
Voorbeeld: Een laserbundel
De bundel van een kleine laboratoriumlaser heeft meestal een intensiteit van ongeveer 1,0 maal 10^{-3} W/m^2). Veronderstel dat de bundel bestaat uit vlakke golven, bereken dan de amplitudes van de elektrische en magnetische velden in de bundel.
Strategie
Gebruik de vergelijking die de intensiteit uitdrukt in termen van het elektrisch veld om het elektrisch veld uit de intensiteit te berekenen.
Oplossing
Uit vergelijking ef{16.31} volgt dat de intensiteit van de laserstraal
De amplitude van het elektrisch veld is dus
&= \sqrt{\frac{2}{(3.00 maal 10^8 m/s(8,85 maal 10^{-12} F/m)}(1,0 maal 10^{-3} W/m^2 rechts)} &= 0,87 \, V/m.
De amplitude van het magnetisch veld kan worden verkregen uit:
Lichtbollenvelden
Een gloeilamp zendt 5,00 W vermogen uit als zichtbaar licht. Wat zijn de gemiddelde elektrische en magnetische velden van het licht op een afstand van 3,0 m?
Strategie
Aanname dat het afgegeven vermogen P van de gloeilamp gelijkmatig is verdeeld over een bol met een straal van 3,0 m om de intensiteit te berekenen, en daaruit het elektrisch veld.
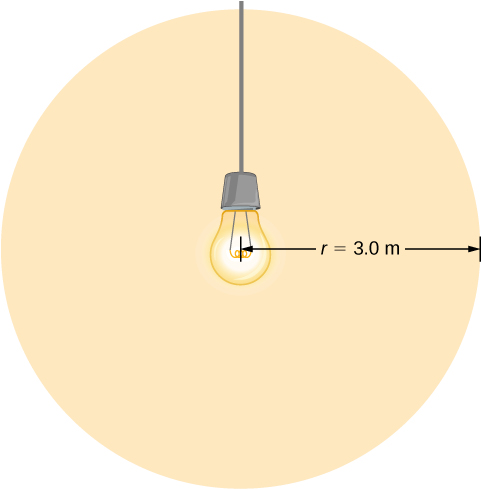
Oplossing
Het vermogen dat als zichtbaar licht wordt uitgestraald, is dan
(I = \frac{P}{4}pi r^2} = \frac{c\epsilon_0 E_0^2}{2},
(E_0 = \sqrt{2\frac{P}{4\pi r^2 cepsilon_0}} = \sqrt{2\frac{5.00 \, W}{4\pi (3,0 \, m)^2 (3,00 \t keer 10^8 \, m/s)(8,85 \t keer 10^{-12} C^2/N \cdot m^2)}} = 5.77 ¤, N/C,¤)
(B_0 = E_0/c = 1,92 ¤ maal 10^{-8} ¤, T).
Betekenis
De intensiteit I neemt af met het kwadraat van de afstand als de straling gelijkmatig in alle richtingen wordt verspreid.
Radiobereik
Een radiozender van 60 kW op aarde zendt zijn signaal naar een satelliet op 100 km afstand (figuur
). Op welke afstand in dezelfde richting zou het signaal dezelfde maximale veldsterkte hebben als het uitgangsvermogen van de zender zou worden opgevoerd tot 90 kW?
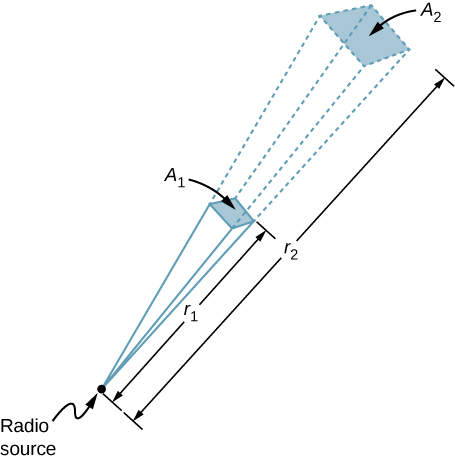
Strategie
Het gebied waarover het vermogen in een bepaalde richting wordt verspreid, neemt toe met het kwadraat van de afstand, zoals geïllustreerd in figuur {(\PageIndex{3}}). Verander het vermogen P met een factor (90 kW/60 kW) en verander de oppervlakte met dezelfde factor om I = \frac{P}{A} = \frac{c\epsilon_0 E_0^2}{2}} gelijk te houden. Gebruik dan de verhouding van oppervlakte A in het diagram tot de afstand in het kwadraat om de afstand te vinden die de berekende verandering in oppervlakte geeft.
Oplossing
Gebruik makend van de evenredigheid van de oppervlakten aan de kwadraten van de afstanden, en oplossend, verkrijgen we uit het diagram
r_2 &= \sqrt{\frac{90}{60}}(100 \, km) \ &= 122 \, km.
Betekenis
Het bereik van een radiosignaal is de maximale afstand tussen zender en ontvanger die een normale werking mogelijk maakt. Als er geen complicaties zijn, zoals reflecties van obstakels, volgt de intensiteit een omgekeerde kwadratenwet, en als het bereik wordt verdubbeld, moet het vermogen met vier worden vermenigvuldigd.
Bijdragers en toeschrijvingen
-
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), en Bill Moebs met vele auteurs die een bijdrage hebben geleverd. Dit werk is gelicenseerd door OpenStax University Physics onder een Creative Commons Naamsvermelding Licentie (by 4.0).