Cele nauczania
Do końca tego rozdziału, będziesz w stanie:
- wyrazić uśrednioną w czasie gęstość energii fal elektromagnetycznych w kategoriach amplitud ich pola elektrycznego i magnetycznego
- obliczyć wektor Poyntinga i natężenie energii fal elektromagnetycznych
- wyjaśnić, jak energia fali elektromagnetycznej zależy od jej amplitudy, podczas gdy energia fotonu jest proporcjonalna do jego częstotliwości
Każdy, kto używał kuchenki mikrofalowej, wie, że w falach elektromagnetycznych jest energia. Czasami ta energia jest oczywista, jak np. w cieple letniego słońca. Innym razem jest ona subtelna, jak np. niewyczuwalna energia promieni gamma, które mogą niszczyć żywe komórki.
Fale elektromagnetyczne wnoszą energię do systemu na mocy swoich pól elektrycznych i magnetycznych. Pola te mogą wywierać siły i poruszać ładunki w systemie, a tym samym wykonywać na nich pracę. Jednakże, istnieje energia w fali elektromagnetycznej sam, czy jest on wchłaniany lub nie. Po utworzeniu, pola przenoszą energię z dala od źródła. Jeśli część energii jest później pochłaniana, natężenie pola maleje, a wszystko, co pozostało, podróżuje dalej.
Jasno widać, że im większe natężenie pola elektrycznego i magnetycznego, tym więcej pracy mogą wykonać i tym większą energię niesie fala elektromagnetyczna. W falach elektromagnetycznych amplituda to maksymalne natężenie pola elektrycznego i magnetycznego (rysunek). Energia fali jest określona przez amplitudę fali.
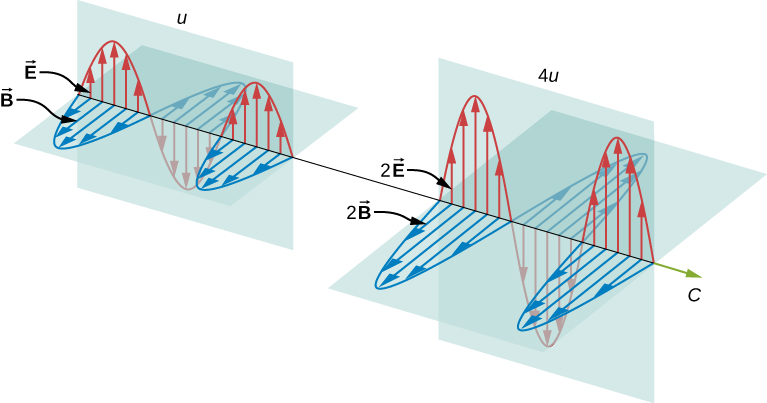
Dla fali płaskiej poruszającej się w kierunku dodatniej osi x, której faza jest tak dobrana, że maksimum fali znajduje się w punkcie początkowym w chwili t = 0, pola elektryczne i magnetyczne spełniają równania
Energia w dowolnej części fali elektromagnetycznej jest sumą energii pól elektrycznych i magnetycznych. Ta energia na jednostkę objętości, lub gęstość energii u, jest sumą gęstości energii z pola elektrycznego i gęstości energii z pola magnetycznego. Wyrażenia dla obu gęstości energii pola zostały omówione wcześniej (\(u_E\) w Pojemność i \(u_B\) w Indukcyjność). Łącząc te składowe otrzymujemy
Wyrażenie \(E = cB = \frac{1}{ \sqrt{\epsilon_0\mu_0}}B\) pokazuje, że gęstość energii magnetycznej \(u_B\) i gęstość energii elektrycznej \(u_E\) są równe, pomimo faktu, że zmieniające się pola elektryczne wytwarzają na ogół tylko małe pola magnetyczne. Równość gęstości energii elektrycznej i magnetycznej prowadzi do
Gęstość energii porusza się wraz z polami elektrycznym i magnetycznym w podobny sposób jak same fale.
Możemy znaleźć szybkość transportu energii rozpatrując mały przedział czasowy \(delta t\). Jak pokazano na rysunku, energia zawarta w walcu o długości c delta t i polu przekroju poprzecznego A przechodzi przez płaszczyznę przekroju poprzecznego w przedziale czasu \(\Delta t\).
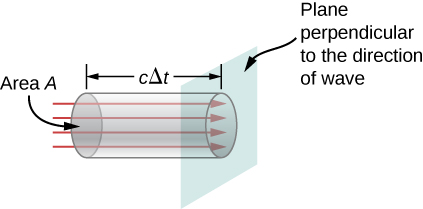
Energia przechodząca przez obszar \(A\) w czasie \(\Delta t\) wynosi
Energia na jednostkę powierzchni w jednostce czasu przechodząca przez płaszczyznę prostopadłą do fali, nazywana strumieniem energii i oznaczana jako \(S), może być obliczona poprzez podzielenie energii przez obszar \(A) i przedział czasu \(Delta t).
Bardziej ogólnie, strumień energii przez dowolną powierzchnię zależy również od jej orientacji. Aby uwzględnić kierunek, wprowadzamy wektor \(\vec{S}\), zwany wektorem Poyntinga, o następującej definicji:
Iloczyn krzyżowy \(\vec{E}) i \(\vec{B}) wskazuje kierunek prostopadły do obu wektorów. Aby potwierdzić, że kierunek \(\vec{S}) jest kierunkiem rozchodzenia się fali, a nie jej ujemnym, wróćmy do Rysunku 16.3.2. Zauważ, że z praw Lenza i Faradaya wynika, że gdy pole magnetyczne rośnie w czasie, to pole elektryczne jest większe w punkcie x niż w punkcie x + delta x. Pole elektryczne maleje wraz ze wzrostem \(x) w danym czasie i miejscu. Proporcjonalność między polem elektrycznym i magnetycznym wymaga, aby pole elektryczne rosło w czasie wraz z polem magnetycznym. Jest to możliwe tylko wtedy, gdy fala rozchodzi się w prawo na wykresie, a w takim przypadku z orientacji względnych wynika, że \(\vec{S} = \frac{1}{\mu_0} \vec{E} \times \) jest konkretnie w kierunku rozchodzenia się fali elektromagnetycznej.
Strumień energii w dowolnym miejscu również zmienia się w czasie, co można zobaczyć, podstawiając ∗(u) z równania 16.3.19 do równania ∗.
Ponieważ częstotliwość światła widzialnego jest bardzo wysoka, rzędu ∗(10^{14} ∗, Hz), strumień energii dla światła widzialnego przechodzący przez dowolny obszar jest wielkością niezwykle szybko zmieniającą się. Większość urządzeń pomiarowych, w tym nasze oczy, wykrywa tylko średnią z wielu cykli. Średnia czasowa strumienia energii jest natężeniem fali elektromagnetycznej i jest mocą na jednostkę powierzchni. Można ją wyrazić przez uśrednienie funkcji cosinus z równania \ref{16.29} w jednym pełnym cyklu, co jest tożsame z uśrednianiem czasowym w wielu cyklach (w tym przypadku ΔT jest jednym okresem):
Możemy albo oszacować całkę, albo zauważyć, że ponieważ sinus i cosinus różnią się tylko fazą, średnia z pełnego cyklu dla \(cos^2 \, (\xi)\) jest taka sama jak dla \(sin^2 \, (\xi)\), aby otrzymać
= \frac{1}{2} \gdzie nawiasy kątowe \(\langle . . . \rangle \) oznaczają operację uśredniania w czasie. Natężenie światła poruszającego się z prędkością ∗ w próżni można zatem określić jako
w kategoriach maksymalnego natężenia pola elektrycznego ∗(E_0}, które jest jednocześnie amplitudą pola elektrycznego. Z algebraicznej manipulacji otrzymujemy zależność
gdzie \(B_0\) jest amplitudą pola magnetycznego, która jest taka sama jak maksymalne natężenie pola magnetycznego. Przydatne jest jeszcze jedno wyrażenie dla \(I_{avg}) w zależności od natężenia pola elektrycznego i magnetycznego. Podstawiając fakt, że cB_0 = E_0, poprzednie wyrażenie staje się
Możemy użyć dowolnego z trzech poprzednich równań, które jest najwygodniejsze, ponieważ te trzy równania są tak naprawdę tylko różnymi wersjami tego samego wyniku: Energia w fali jest związana z amplitudą podniesioną do kwadratu. Ponadto, ponieważ równania te opierają się na założeniu, że fale elektromagnetyczne są sinusoidalne, natężenie szczytowe jest dwa razy większe od natężenia średniego; to znaczy, że I_0 = 2I}.
Przykład: Wiązka laserowa
Wiązka z małego lasera laboratoryjnego ma zwykle natężenie około \(1,0 \ razy 10^{-3} W/m^2\). Zakładając, że wiązka składa się z fal płaskich, oblicz amplitudy pól elektrycznych i magnetycznych w wiązce.
Strategia
Użyj równania wyrażającego natężenie w kategoriach pola elektrycznego, aby obliczyć pole elektryczne na podstawie natężenia.
Rozwiązanie
Z równania ^16.31} wynika, że natężenie wiązki laserowej wynosi
Amplituda pola elektrycznego wynosi zatem
&= ^sqrt{ ^frac{2}{(3.00 ^times 10^8 m/s)(8.85 ^times 10^{-12} F/m)} \left(1.0 ^times 10^{-3} W/m^2 \right)} \\ &= 0,87 \, V/m. \end{align*}]
Amplitudę pola magnetycznego można otrzymać z:
Pole żarówki
Żarówka emituje 5,00 W mocy w postaci światła widzialnego. Jakie są średnie pola elektryczne i magnetyczne pochodzące od tego światła w odległości 3,0 m?
Strategia
Zakładając, że moc wyjściowa żarówki P rozkłada się równomiernie na sferę o promieniu 3,0 m, oblicz natężenie, a z niego pole elektryczne.
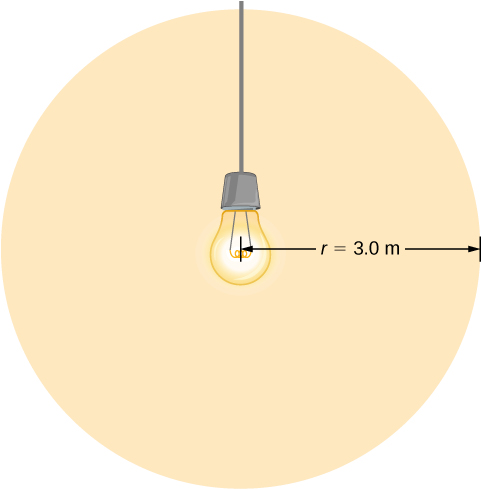
Rozwiązanie
Moc wypromieniowana w postaci światła widzialnego wynosi wtedy
(I = \frac{P}{4\pi r^2} = \frac{c\epsilon_0 E_0^2}{2}\)
(E_0 = \sqrt{2\frac{P}{4\pi r^2 c\epsilon_0}} = \sqrt{2\frac{5.00 \, W}{4\pi (3,0 \, m)^2 (3,00 \times 10^8 \, m/s)(8,85 \times 10^{-12} C^2/N \cdot m^2)}} = 5.77 \, N/C,\)
(B_0 = E_0/c = 1,92 \times 10^{-8} \, T).
Znaczenie
Intensywność I spada wraz z kwadratem odległości, jeśli promieniowanie jest rozproszone równomiernie we wszystkich kierunkach.
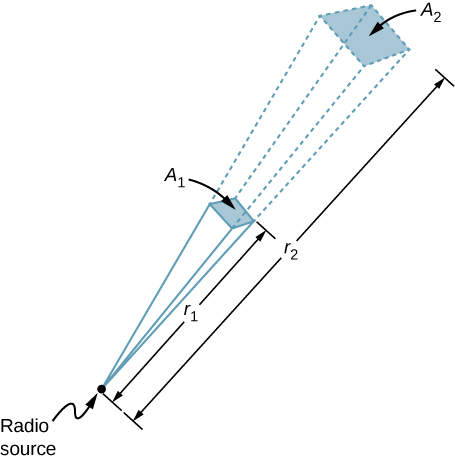
Zasięg promieniowania radiowego
Nadajnik radiowy o mocy 60 kW na Ziemi wysyła swój sygnał do satelity odległego o 100 km (rysunek rzedu{3}). W jakiej odległości w tym samym kierunku sygnał miałby takie samo maksymalne natężenie pola, gdyby moc wyjściowa nadajnika została zwiększona do 90 kW?
Strategia
Obszar, na którym rozpraszana jest moc w danym kierunku, rośnie wraz z kwadratem odległości, jak pokazano na rysunku \(\PageIndex{3}}). Zmień moc wyjściową P o współczynnik (90 kW/60 kW) i zmień powierzchnię o ten sam współczynnik, tak aby \(I = \frac{P}{A} = \frac{c\epsilon_0 E_0^2}{2}}) pozostała taka sama. Następnie użyj proporcji pola powierzchni A na wykresie do odległości podniesionej do kwadratu, aby znaleźć odległość, która powoduje obliczoną zmianę pola powierzchni.
Rozwiązanie
Korzystając z proporcjonalności obszarów do kwadratów odległości i rozwiązując, otrzymujemy na podstawie wykresu
r_2 &= \sqrt{frac{90}{60}}(100 \, km) \{&
= 122 \, km. \end{align*}]
Znaczenie
Zasięg sygnału radiowego to maksymalna odległość między nadajnikiem a odbiornikiem, która pozwala na normalną pracę. W przypadku braku komplikacji, takich jak odbicia od przeszkód, natężenie sygnału jest zgodne z prawem odwrotności kwadratu, a podwojenie zasięgu wymagałoby pomnożenia mocy przez cztery.
Wydawcy i przypisy
-
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University) i Bill Moebs wraz z wieloma autorami. Ta praca jest licencjonowana przez OpenStax University Physics na licencji Creative Commons Attribution License (by 4.0).