Objetivos de aprendizaje
Al finalizar esta sección, serás capaz de:
- Expresar la densidad de energía promediada en el tiempo de las ondas electromagnéticas en términos de sus amplitudes de campo eléctrico y magnético
- Calcular el vector de Poynting y la intensidad de energía de las ondas electromagnéticas
- Explicar cómo la energía de una onda electromagnética depende de su amplitud, mientras que la energía de un fotón es proporcional a su frecuencia
Cualquiera que haya utilizado un horno microondas sabe que hay energía en las ondas electromagnéticas. A veces esta energía es evidente, como en el calor del Sol en verano. Otras veces, es sutil, como la energía no sentida de los rayos gamma, que pueden destruir células vivas.
Las ondas electromagnéticas aportan energía a un sistema en virtud de sus campos eléctricos y magnéticos. Estos campos pueden ejercer fuerzas y mover cargas en el sistema y, por tanto, realizar un trabajo sobre ellas. Sin embargo, hay energía en una onda electromagnética en sí misma, tanto si es absorbida como si no. Una vez creados, los campos transportan energía desde una fuente. Si más tarde se absorbe algo de energía, las intensidades de los campos disminuyen y todo lo que queda sigue viajando.
Claramente, cuanto mayor sea la fuerza de los campos eléctricos y magnéticos, más trabajo pueden hacer y mayor es la energía que transporta la onda electromagnética. En las ondas electromagnéticas, la amplitud es la máxima intensidad de los campos eléctrico y magnético (Figura \(\PageIndex{1})). La energía de la onda viene determinada por la amplitud de la misma.
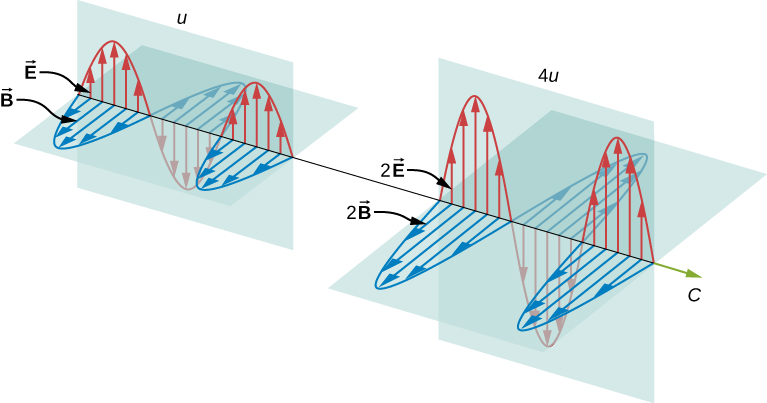
Para una onda plana que viaja en la dirección del eje x positivo con la fase de la onda elegida de forma que el máximo de la onda se encuentre en el origen en \N(t = 0\), los campos eléctrico y magnético obedecen a las ecuaciones
La energía en cualquier parte de la onda electromagnética es la suma de las energías de los campos eléctrico y magnético. Esta energía por unidad de volumen, o densidad de energía u, es la suma de la densidad de energía del campo eléctrico y la densidad de energía del campo magnético. Las expresiones para ambas densidades de energía de campo se discutieron anteriormente (\(u_E\) en Capacitancia y \(u_B\) en Inductancia). Combinando estas contribuciones, obtenemos
La expresión \(E = cB = \frac{1}{{sqrt{epsilon_0\mu_0}B\) muestra entonces que la densidad de energía magnética \(u_B\) y la densidad de energía eléctrica \(u_E\) son iguales, a pesar de que los campos eléctricos cambiantes generalmente producen sólo pequeños campos magnéticos. La igualdad de las densidades de energía eléctrica y magnética conduce a que
La densidad de energía se mueve con los campos eléctricos y magnéticos de forma similar a las propias ondas.
Podemos encontrar la tasa de transporte de energía considerando un pequeño intervalo de tiempo \(\Delta t\). Como se muestra en la Figura \(\PageIndex{2}), la energía contenida en un cilindro de longitud \(c\Delta t\) y área transversal A pasa por el plano de la sección transversal en el intervalo \(\Delta t\).
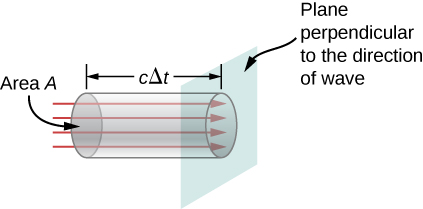
La energía que pasa a través del área \(A\) en el tiempo \(\Delta t\) es
La energía por unidad de área por unidad de tiempo que pasa a través de un plano perpendicular a la onda, llamada flujo de energía y denotada por \(S\), se puede calcular dividiendo la energía por el área \(A\) y el intervalo de tiempo \(\Delta t\).
De forma más general, el flujo de energía a través de cualquier superficie depende también de la orientación de la misma. Para tener en cuenta la dirección, introducimos un vector \(\vec{S}\), llamado vector Poynting, con la siguiente definición:
El producto cruzado de \(\vec{E}\) y \(\vec{B}\) apunta en la dirección perpendicular a ambos vectores. Para confirmar que la dirección de \(\vec{S}\) es la de la propagación de la onda, y no su negativo, volvamos a la figura 16.3.2. Observe que las leyes de Lenz y Faraday implican que cuando el campo magnético mostrado es creciente en el tiempo, el campo eléctrico es mayor en \(x\) que en \(x + \Delta x\). El campo eléctrico es decreciente al aumentar \(x\) en el tiempo y lugar dados. La proporcionalidad entre los campos eléctricos y magnéticos requiere que el campo eléctrico aumente en el tiempo junto con el campo magnético. Esto sólo es posible si la onda se propaga hacia la derecha en el diagrama, en cuyo caso, las orientaciones relativas muestran que \(\vec{S} = \frac{1}{mu_0} \vec{E} \times \vec{B}\) está específicamente en la dirección de propagación de la onda electromagnética.
El flujo de energía en cualquier lugar también varía en el tiempo, como se puede ver sustituyendo \(u\) de la ecuación 16.3.19 en la ecuación \ref{16.27}.
Debido a que la frecuencia de la luz visible es muy alta, del orden de \(10^{14} \\ Hz\), el flujo de energía para la luz visible a través de cualquier área es una cantidad que varía extremadamente rápido. La mayoría de los dispositivos de medición, incluidos nuestros ojos, sólo detectan un promedio a lo largo de muchos ciclos. La media temporal del flujo de energía es la intensidad \ (I\) de la onda electromagnética y es la potencia por unidad de superficie. Puede expresarse promediando la función coseno de la ecuación \ref{16.29} a lo largo de un ciclo completo, que es lo mismo que promediar el tiempo a lo largo de muchos ciclos (aquí, \(T\) es un período):
Podemos evaluar la integral, o bien observar que debido a que el seno y el coseno difieren meramente en la fase, el promedio sobre un ciclo completo para \(cos^2 \, (\xi)\) es el mismo que para \(sin^2 \, (\xi)\), para obtener
= \frac{1}{2} \langle 1 \rangle = \frac{1}{2}.\]
donde los paréntesis angulares \(\langle . . \rangle \) representan la operación de promediación del tiempo. La intensidad de la luz que se mueve a la velocidad \(c\) en el vacío se encuentra entonces
en términos de la intensidad máxima del campo eléctrico \(E_0\), que es también la amplitud del campo eléctrico. La manipulación algebraica produce la relación
donde \(B_0\) es la amplitud del campo magnético, que es la misma que la intensidad máxima del campo magnético. Resulta útil una expresión más para \(I_{avg}\Nen términos de las intensidades de campo eléctrico y magnético. Sustituyendo el hecho de que \(cB_0 = E_0\), la expresión anterior se convierte en
Podemos utilizar cualquiera de las tres ecuaciones anteriores que sea más conveniente, porque las tres ecuaciones son realmente sólo diferentes versiones del mismo resultado: La energía de una onda está relacionada con la amplitud al cuadrado. Además, como estas ecuaciones se basan en la suposición de que las ondas electromagnéticas son sinusoidales, la intensidad máxima es el doble de la intensidad media; es decir, \(I_0 = 2I\).
Ejemplo \(\PageIndex{1}\): Un rayo láser
El rayo de un pequeño láser de laboratorio suele tener una intensidad de aproximadamente \(1,0 \times 10^{-3} W/m^2\). Suponiendo que el haz está compuesto por ondas planas, calcule las amplitudes de los campos eléctrico y magnético en el haz.
Estrategia
Utilice la ecuación que expresa la intensidad en términos del campo eléctrico para calcular el campo eléctrico a partir de la intensidad.
Solución
A partir de la ecuación \ref{16.31}, la intensidad del rayo láser es
La amplitud del campo eléctrico es por tanto
&= \frac{2}(3.00 \times 10^8 m/s)(8,85 \times 10^{-12} F/m)}left(1,0 \times 10^{-3} W/m^2 \right)} &= 0,87 V/m. \end{align*}]
La amplitud del campo magnético puede obtenerse a partir de:
Campos de la bombilla
Una bombilla emite 5,00 W de potencia como luz visible. ¿Cuáles son los campos eléctrico y magnético medios de la luz a una distancia de 3,0 m?
Estrategia
Suponga que la potencia P de la bombilla se distribuye uniformemente sobre una esfera de radio 3,0 m para calcular la intensidad, y a partir de ella, el campo eléctrico.
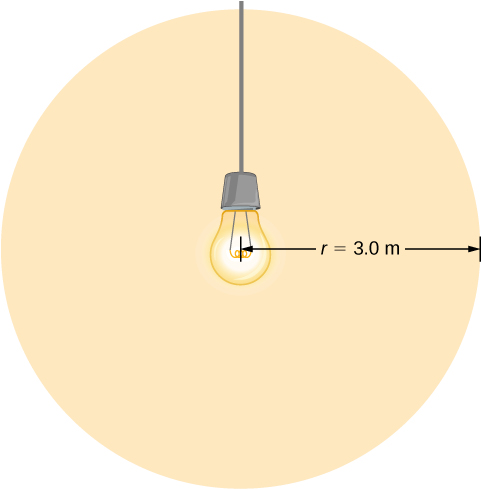
Solución
La potencia radiada como luz visible es entonces
(I = \frac{P}{4\pi r^2} = \frac{c\epsilon_0 E_0^2}{2},
(E_0 = \frac{P}{4\pi r^2 c\epsilon_0} = \sqrt{2\frac{5.00 \, W}{4\pi (3,0 \, m)^2 (3,00 \times 10^8 \, m/s)(8,85 \times 10^{-12} C^2/N \cdot m^2)}} = 5.77 \, N/C,\})
(B_0 = E_0/c = 1,92 \times 10^{-8} \, T\).
Significado
La intensidad I decae con la distancia al cuadrado si la radiación se dispersa uniformemente en todas las direcciones.
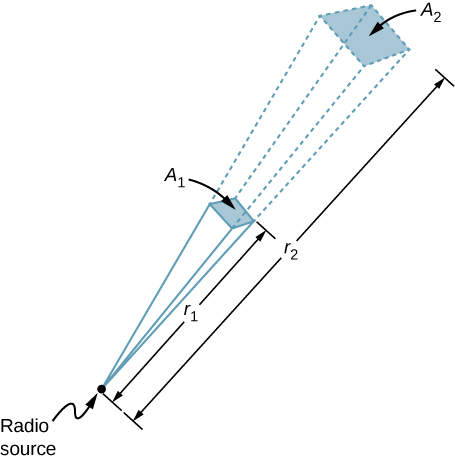
Un transmisor de radio de 60 kW en la Tierra envía su señal a un satélite situado a 100 km de distancia (Figura \(\PageIndex{3}\)). ¿A qué distancia en la misma dirección tendría la señal la misma intensidad de campo máxima si la potencia de salida del transmisor se aumentara a 90 kW?
Estrategia
El área sobre la que se dispersa la potencia en una dirección concreta aumenta con la distancia al cuadrado, como se ilustra en la figura \(\PageIndex{3}\). Cambie la potencia de salida P por un factor de (90 kW/60 kW) y cambie el área por el mismo factor para mantener \ ~(I = \frac{P}{A} = \frac{c\epsilon_0 E_0^2}{2}) igual. A continuación, utilice la proporción del área A en el diagrama a la distancia al cuadrado para encontrar la distancia que produce el cambio calculado en el área.
Solución
Utilizando la proporcionalidad de las áreas a los cuadrados de las distancias, y resolviendo, obtenemos a partir del diagrama
\NR_2 &= \Nsqrt{\Nfrac{90}{60}(100 \Nkm) \N &= 122 \Nkm. \end{align*}]
Significado
El alcance de una señal de radio es la distancia máxima entre el emisor y el receptor que permite un funcionamiento normal. En ausencia de complicaciones como las reflexiones de los obstáculos, la intensidad sigue una ley del cuadrado inverso, y duplicar el alcance requeriría multiplicar la potencia por cuatro.
Contribuidores y atribuciones
-
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), y Bill Moebs con muchos autores colaboradores. Esta obra está licenciada por OpenStax University Physics bajo una Licencia de Atribución de Creative Commons (por 4.0).