Lärandemål
I slutet av det här avsnittet kommer du att kunna:
- Uttryck den tidsmedelvärdesberäknade energitätheten hos elektromagnetiska vågor i termer av deras elektriska och magnetiska fältamplituder
- Beräkna Poyntingvektorn och energiintensiteten hos elektromagnetiska vågor
- Förklara hur energin hos en elektromagnetisk våg beror på amplituden, medan energin hos en foton är proportionell mot frekvensen
Var och en som har använt en mikrovågsugn vet att det finns energi i elektromagnetiska vågor. Ibland är denna energi uppenbar, till exempel i sommarsolens värme. Andra gånger är den subtil, till exempel den obetydliga energin i gammastrålar, som kan förstöra levande celler.
Elektromagnetiska vågor för in energi i ett system i kraft av sina elektriska och magnetiska fält. Dessa fält kan utöva krafter och flytta laddningar i systemet och därmed utföra arbete på dem. Det finns dock energi i själva en elektromagnetisk våg, oavsett om den absorberas eller inte. När fälten väl har skapats transporterar de energi bort från en källa. Om en del energi senare absorberas minskar fältstyrkorna och det som finns kvar färdas vidare.
Det är tydligt att ju större styrkan hos de elektriska och magnetiska fälten är, desto mer arbete kan de utföra och desto större energi bär den elektromagnetiska vågen. I elektromagnetiska vågor är amplituden den maximala fältstyrkan hos de elektriska och magnetiska fälten (figur \(\PageIndex{1}\)). Vågens energi bestäms av vågens amplitud.
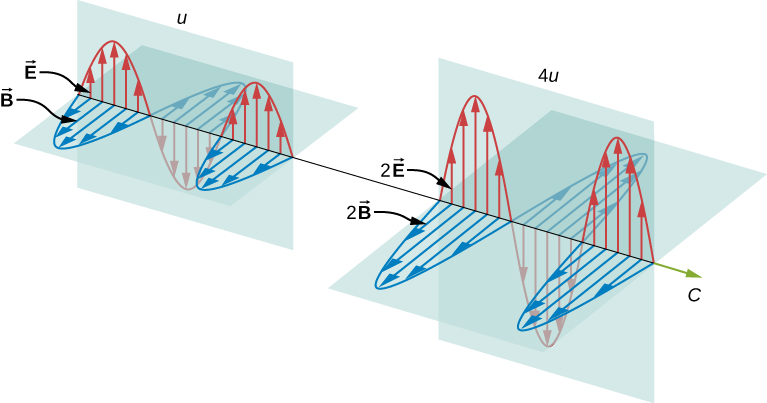
För en plan våg som färdas i riktning mot den positiva x-axeln med vågens fas vald så att vågmaximum är vid ursprunget vid \(t = 0\), följer de elektriska och magnetiska fälten ekvationerna
\
Energin i varje del av den elektromagnetiska vågen är summan av energin i de elektriska och magnetiska fälten. Denna energi per volymenhet, eller energitäthet u, är summan av energitätheten från det elektriska fältet och energitätheten från det magnetiska fältet. Uttrycken för båda energitätheterna i fälten har diskuterats tidigare (\(u_E\) i kapacitans och \(u_B\) i induktans). Genom att kombinera dessa bidrag får vi
\\
Uttrycket \(E = cB = \frac{1}{\sqrt{\epsilon_0\mu_0}}}B\) visar sedan att den magnetiska energitätheten \(u_B\) och den elektriska energitätheten \(u_E\) är lika stora, trots att förändrade elektriska fält generellt sett bara ger upphov till små magnetiska fält. Jämlikheten mellan de elektriska och magnetiska energitätheterna leder till
\
Energitätheten rör sig med de elektriska och magnetiska fälten på samma sätt som vågorna själva.
Vi kan hitta transporthastigheten för energin genom att betrakta ett litet tidsintervall \(\Delta t\). Som visas i figur \(\PageIndex{2}\) passerar energin i en cylinder med längden \(c\Delta t\) och tvärsnittsytan A genom tvärsnittsplanet i intervallet \(\Delta t\).
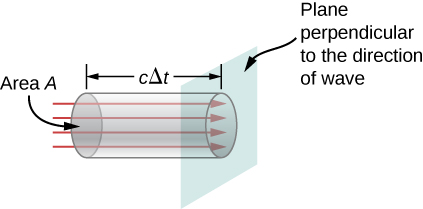
Energin som passerar genom området \(A\) i tiden \(\Delta t\) är
\\
Energin per ytenhet per tidsenhet som passerar genom ett plan vinkelrätt mot vågen, som kallas energiflödet och betecknas \(S\), kan beräknas genom att dividera energin med arean \(A\) och tidsintervallet \(\Delta t\).
Mer generellt sett beror energiflödet genom en yta också på ytans orientering. För att ta hänsyn till riktningen inför vi en vektor \(\vec{S}\), kallad Poyntingvektorn, med följande definition:
Korsningsprodukten av \(\vec{E}\) och \(\vec{B}\) pekar i den riktning som är vinkelrät mot båda vektorerna. För att bekräfta att riktningen för \(\vec{S}\) är vågutbredningens riktning, och inte dess negativ, återgå till figur 16.3.2. Observera att Lenz’ och Faradays lagar innebär att när det visade magnetfältet ökar med tiden är det elektriska fältet större vid \(x\) än vid \(x + \Delta x\). Det elektriska fältet minskar med ökande \(x\) vid den givna tiden och platsen. Proportionaliteten mellan elektriska och magnetiska fält kräver att det elektriska fältet ökar med tiden tillsammans med det magnetiska fältet. Detta är endast möjligt om vågen utbreder sig till höger i diagrammet, i vilket fall de relativa orienteringarna visar att \(\vec{S} = \frac{1}{\mu_0} \vec{E} \times \vec{B}\) är specifikt i den elektromagnetiska vågens utbredningsriktning.
Energiflödet på varje plats varierar också i tiden, vilket framgår genom att ersätta \(u\) från ekvation 16.3.19 med ekvation \ref{16.27}.
\
Med tanke på att frekvensen för det synliga ljuset är mycket hög, i storleksordningen \(10^{14} \, Hz\), är energiflödet för det synliga ljuset genom varje område en extremt snabbt varierande storhet. De flesta mätinstrument, inklusive våra ögon, registrerar endast ett medelvärde över många cykler. Tidsgenomsnittet av energiflödet är den elektromagnetiska vågens intensitet \(I\) och är effekten per ytenhet. Den kan uttryckas genom att medelvärdesberäkna cosinusfunktionen i ekvation \ref{16.29} över en hel cykel, vilket är samma sak som att tidsmitta över många cykler (här är \(T\) en period):
Vi kan antingen utvärdera integralen eller notera att eftersom sinus och cosinus endast skiljer sig åt i fas är medelvärdet över en hel cykel för \(cos^2 \, (\xi)\) detsamma som för \(sin^2 \, (\xi)\), för att få
\ = \frac{1}{2} \langle 1 \rangle = \frac{1}{2}.\]
där vinkelparenteserna \(\langle . . . \rangle \) står för tidsmedelvärdesoperationen. Intensiteten hos ljus som rör sig med hastigheten \(c\) i vakuum finner man då
\\
i termer av den maximala elektriska fältstyrkan \(E_0\), som också är det elektriska fältets amplitud. Algebraisk manipulation ger sambandet
\
där \(B_0\) är magnetfältsamplituden, som är densamma som den maximala magnetfältsstyrkan. Ytterligare ett uttryck för \(I_{avg}\) i termer av både elektriska och magnetiska fältstyrkor är användbart. Genom att ersätta det faktum att \(cB_0 = E_0\) blir det föregående uttrycket
\
Vi kan använda vilken av de tre föregående ekvationerna som är lämpligast, eftersom de tre ekvationerna egentligen bara är olika versioner av samma resultat: Energin i en våg är relaterad till amplituden i kvadrat. Eftersom dessa ekvationer dessutom bygger på antagandet att de elektromagnetiska vågorna är sinusformade är toppintensiteten dubbelt så stor som den genomsnittliga intensiteten; det vill säga \(I_0 = 2I\).
Exempel \(\PageIndex{1}\): En laserstråle
Strålen från en liten laboratorielaser har vanligtvis en intensitet på cirka \(1,0 \ gånger 10^{-3} W/m^2\). Om man antar att strålen består av plana vågor, beräkna amplituderna av de elektriska och magnetiska fälten i strålen.
Strategi
Använd ekvationen som uttrycker intensiteten i termer av det elektriska fältet för att beräkna det elektriska fältet från intensiteten.
Lösning
Från ekvation \ref{16.31} är laserstrålens intensitet
\
Amplituden för det elektriska fältet är därför
\\ &= \sqrt{\frac{2}{(3.00 \times 10^8 m/s)(8.85 \times 10^{-12} F/m)}\left(1.0 \times 10^{-3} W/m^2 \right)} \\ &= 0,87 \, V/m. \end{align*}\]
Magnetfältets amplitud kan erhållas från:
\
Fält från glödlampor
En glödlampa avger 5,00 W effekt som synligt ljus. Vilka är de genomsnittliga elektriska och magnetiska fälten från ljuset på ett avstånd av 3,0 m?
Strategi
Antag att glödlampans uteffekt P är jämnt fördelad över en sfär med radien 3,0 m för att beräkna intensiteten, och därifrån det elektriska fältet.
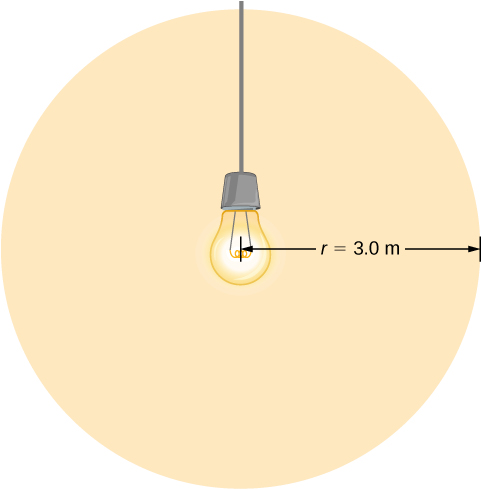
Lösning
Den effekt som strålar ut som synligt ljus är då
\(I = \frac{P}{4\pi r^2} = \frac{c\epsilon_0 E_0^2}{2},\)
\(E_0 = \sqrt{2\frac{P}{4\pi r^2 c\epsilon_0}} = \sqrt{2\frac{5.00 \, W}{4\pi (3.0 \, m)^2 (3.00 \times 10^8 \, m/s)(8.85 \times 10^{-12} C^2/N \cdot m^2)}} = 5.77 \, N/C,\)
\(B_0 = E_0/c = 1,92 \times 10^{-8} \, T\).
Betydelse
Intensiteten I avtar med avståndet i kvadrat om strålningen sprids jämnt i alla riktningar.
Radioavstånd
En radiosändare på 60 kW på jorden sänder sin signal till en satellit 100 km bort (figur \(\PageIndex{3}\)). På vilket avstånd i samma riktning skulle signalen ha samma maximala fältstyrka om sändarens uteffekt ökades till 90 kW?
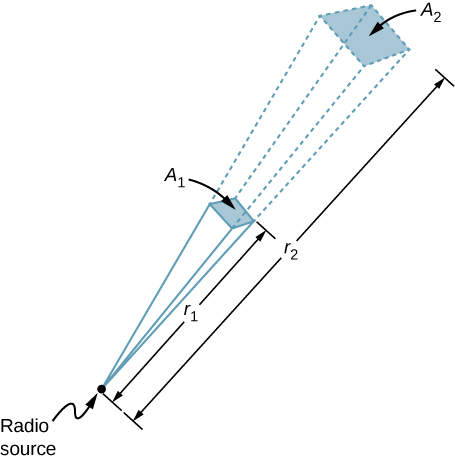
Strategi
Området över vilket kraften i en viss riktning sprids ökar med avståndet i kvadrat, vilket illustreras i figur \(\PageIndex{3}\). Ändra effekten P med en faktor (90 kW/60 kW) och ändra ytan med samma faktor för att hålla \(I = \frac{P}{A} = \frac{c\epsilon_0 E_0^2}{2}\) oförändrad. Använd sedan förhållandet mellan arean A i diagrammet och avståndet i kvadrat för att hitta det avstånd som ger den beräknade förändringen av arean.
Lösning
Med hjälp av proportionaliteten mellan areorna och kvadraterna på avstånden och genom att lösa får vi från diagrammet
\\ r_2 &= \sqrt{\frac{90}{60}}(100 \, km) \\ &= 122 \, km. \end{align*}\]
Betydelse
Räckvidden för en radiosignal är det maximala avståndet mellan sändare och mottagare som möjliggör normal drift. I avsaknad av komplikationer som reflektioner från hinder följer intensiteten en omvänd kvadratisk lag, och för att fördubbla räckvidden skulle man behöva multiplicera effekten med fyra.
Kontributer och tillskrivningar
-
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University) och Bill Moebs med många medverkande författare. Detta arbete är licensierat av OpenStax University Physics under en Creative Commons Attribution License (by 4.0).